题目内容
直线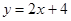 与抛物线
与抛物线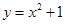 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )
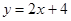 与抛物线
与抛物线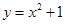 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )A.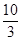 | B.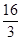 | C.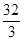 | D.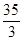 |
C
试题分析:联立直线与抛物线解析式
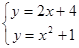 ,得:
,得: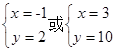 ,设直线
,设直线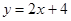 与抛物线
与抛物线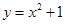 所围成图形的面积为S,所以
所围成图形的面积为S,所以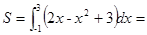
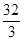 。
。点评:此题考查了定积分的运算及数形结合的思想,熟练掌握利用定积分表示封闭图形的面积是解本题的关键.

练习册系列答案
相关题目
题目内容
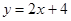 与抛物线
与抛物线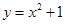 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )A.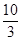 | B.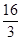 | C.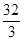 | D.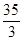 |
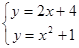 ,得:
,得: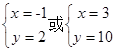 ,设直线
,设直线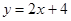 与抛物线
与抛物线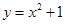 所围成图形的面积为S,所以
所围成图形的面积为S,所以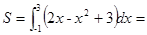
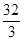 。
。