题目内容
如图,有6个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(4,0),O4(0,2),O5(2,2),O6(4,2).记集合M={⊙Oi|i=1,2,3,4,5,6}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中 “有序集合对”(A,B) 的个数是
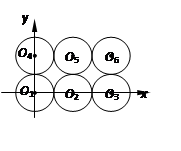
| A.50 | B.54 | C.58 | D.60 |
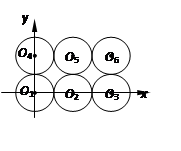
B
若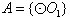 ,则集合
,则集合 是集合
是集合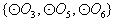 的非空子集,有
的非空子集,有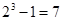 种可能。
种可能。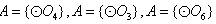 的情况类似,则总共有4×7=28个“有序集合对”;
的情况类似,则总共有4×7=28个“有序集合对”;
若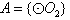 ,则集合
,则集合 是集合
是集合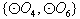 的非空子集,有
的非空子集,有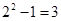 种可能。
种可能。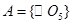 的情况类似,则总共有2×3=6个“有序集合对”;
的情况类似,则总共有2×3=6个“有序集合对”;
若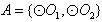 ,则集合
,则集合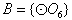 只有1种可能。
只有1种可能。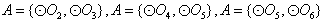 的情况类似,则总共有4×1=4个“有序集合对”;
的情况类似,则总共有4×1=4个“有序集合对”;
若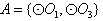 ,则集合
,则集合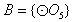 只有1种可能。
只有1种可能。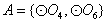 的情况类似,则总共有2×1=2个“有序集合对”;
的情况类似,则总共有2×1=2个“有序集合对”;
若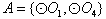 ,则集合
,则集合 是集合
是集合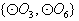 的非空子集,有
的非空子集,有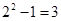 种可能。
种可能。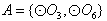 的情况类似,而
的情况类似,而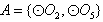 与其他圆均有公共点此时不存在集合
与其他圆均有公共点此时不存在集合 ,则总共有2×3=6个“有序集合对”;
,则总共有2×3=6个“有序集合对”;
若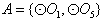 ,则集合
,则集合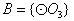 只有1种可能。
只有1种可能。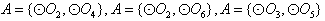 的情况类似,则总共有4×1=4个“有序集合对”;
的情况类似,则总共有4×1=4个“有序集合对”;
若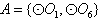 ,此时与其他圆均有公共点此时不存在集合
,此时与其他圆均有公共点此时不存在集合 。
。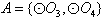 的情况类似,则总共有0个“有序集合对”;
的情况类似,则总共有0个“有序集合对”;
若集合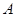 中有3个元素时,则只有当,
中有3个元素时,则只有当,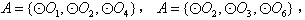
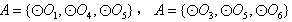 情况下,集合
情况下,集合 对应有1种可能,其他情况下均与其他圆均有公共点此时不存在集合
对应有1种可能,其他情况下均与其他圆均有公共点此时不存在集合 。则总共有4×1=4个“有序集合对”;
。则总共有4×1=4个“有序集合对”;
若集合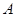 中有4个以上元素时,均与其他圆均有公共点此时不存在集合
中有4个以上元素时,均与其他圆均有公共点此时不存在集合 。则不存在“有序集合对”。
。则不存在“有序集合对”。
综上可得,总共有28+6+4+2+6+4+4=54个“有序集合对”,故选B
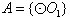 ,则集合
,则集合 是集合
是集合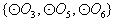 的非空子集,有
的非空子集,有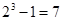 种可能。
种可能。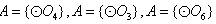 的情况类似,则总共有4×7=28个“有序集合对”;
的情况类似,则总共有4×7=28个“有序集合对”;若
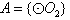 ,则集合
,则集合 是集合
是集合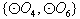 的非空子集,有
的非空子集,有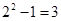 种可能。
种可能。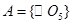 的情况类似,则总共有2×3=6个“有序集合对”;
的情况类似,则总共有2×3=6个“有序集合对”;若
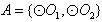 ,则集合
,则集合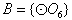 只有1种可能。
只有1种可能。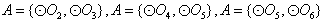 的情况类似,则总共有4×1=4个“有序集合对”;
的情况类似,则总共有4×1=4个“有序集合对”;若
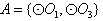 ,则集合
,则集合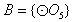 只有1种可能。
只有1种可能。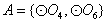 的情况类似,则总共有2×1=2个“有序集合对”;
的情况类似,则总共有2×1=2个“有序集合对”;若
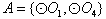 ,则集合
,则集合 是集合
是集合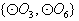 的非空子集,有
的非空子集,有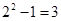 种可能。
种可能。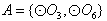 的情况类似,而
的情况类似,而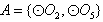 与其他圆均有公共点此时不存在集合
与其他圆均有公共点此时不存在集合 ,则总共有2×3=6个“有序集合对”;
,则总共有2×3=6个“有序集合对”;若
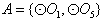 ,则集合
,则集合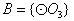 只有1种可能。
只有1种可能。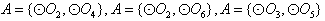 的情况类似,则总共有4×1=4个“有序集合对”;
的情况类似,则总共有4×1=4个“有序集合对”;若
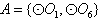 ,此时与其他圆均有公共点此时不存在集合
,此时与其他圆均有公共点此时不存在集合 。
。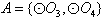 的情况类似,则总共有0个“有序集合对”;
的情况类似,则总共有0个“有序集合对”;若集合
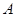 中有3个元素时,则只有当,
中有3个元素时,则只有当,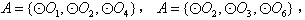
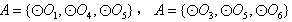 情况下,集合
情况下,集合 对应有1种可能,其他情况下均与其他圆均有公共点此时不存在集合
对应有1种可能,其他情况下均与其他圆均有公共点此时不存在集合 。则总共有4×1=4个“有序集合对”;
。则总共有4×1=4个“有序集合对”;若集合
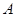 中有4个以上元素时,均与其他圆均有公共点此时不存在集合
中有4个以上元素时,均与其他圆均有公共点此时不存在集合 。则不存在“有序集合对”。
。则不存在“有序集合对”。综上可得,总共有28+6+4+2+6+4+4=54个“有序集合对”,故选B

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
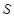 是实数集
是实数集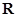 的非空子集,如果
的非空子集,如果 有
有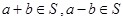 ,则称
,则称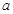 ,集合
,集合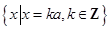 都是“和谐集”
都是“和谐集”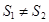 ,且
,且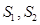 均是“和谐集”,则
均是“和谐集”,则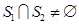
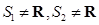 ,则
,则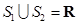
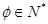

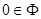
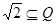
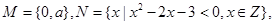 若
若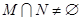 ,则
,则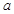 的值为
的值为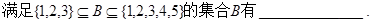
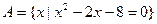 ,
,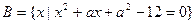 ,
,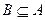 ,求a的取值范围。
,求a的取值范围。 ,
, ,
, ,则
,则 是( )
是( )
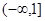
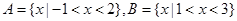 ,那么
,那么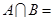 ( )
( )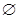
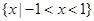
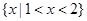
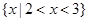
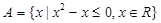 ,集合
,集合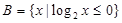 ,则
,则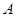 、
、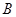 满足( )
满足( )
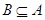
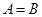
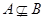 且
且