题目内容
 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
①求证:平面ADE⊥平面ABE;
②求点C到平面ADE的距离.
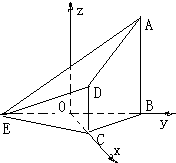 解法1:①取BE的中点O,连OC.
解法1:①取BE的中点O,连OC.∵BC=CE,∴OC⊥BE.又AB⊥平面BCE.
以O为原点建立空间直角坐标系O-xyz如图,
则由已知条件有:C(1,0,0),
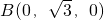 ,
, D(1,0,1),
D(1,0,1), (4分)
(4分)设平面ADE的法向量为n=(a,b,c),
则由n•
 =
=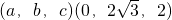 =
=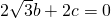 .
.及n•
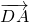 =
= =
=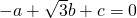 .
.可取
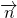 =
=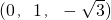 (6分)
(6分)又AB⊥平面BCE.
∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取为
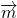 =(1,0,0).
=(1,0,0).∵
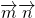 =
=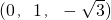 •(1,0,0)=0,
•(1,0,0)=0,∴
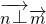
∴平面ADE⊥平面ABE.(8分)
②点C到平面ADE的距离为
 (12分)
(12分)解法2:①取BE的中点O,AE的中点F,连OC,OF,CD.则OF



∵AB⊥平面BCE,CD⊥平面BCE,AB=2CD
∴CD

 ,OF
,OF CD
CD∴OC∥FD (3分)
∵BC=CE,
∴OC⊥BE.又AB⊥平面BCE.
∴OC⊥平面ABE.
∴FD⊥平面ABE.
从而平面ADE⊥平面ABE.(6分)
②∵CD

 ,延长AD,BC交于T
,延长AD,BC交于T则C为BT的中点.
点C到平面ADE的距离等于点B到平面ADE的距离的
 .(8分)
.(8分)过B作BH⊥AE,垂足为H.
∵平面ADE.⊥平面ABE.
∴BH⊥平面BDE.
由已知有AB⊥BE.BE=
 ,AB=2,
,AB=2,∴BH=
 ,
,从而点C到平面ADE的距离为
 (12分)
(12分)分析:解法1①取BE的中点O,连OC.BC=CE,OC⊥BE.又AB⊥平面BCE,以O为原点建立空间直角坐标系O-xyz.写出要用的点的坐标,表示出两个平面的法向量,根据两个法向量垂直得到面面垂直.
②根据写出的点的坐标,得到直线对应的向量的坐标,根据两个向量之间所成的角得到线面角.
解法2①做出辅助线,取BE的中点O,AE的中点F,连OC,OF,CD,AB⊥平面BCE,CD⊥平面BCE,根据线面垂直得到面面垂直.
②根据CD

 ,延长AD,BC交于T,得到C为BT的中点.得到点C到平面ADE的距离等于点B到平面ADE的距离的
,延长AD,BC交于T,得到C为BT的中点.得到点C到平面ADE的距离等于点B到平面ADE的距离的 ,做出结果.
,做出结果.点评:本题考查线面垂直和点到面的距离,本题求距离也可以这样解:OC∥FD,点C到平面ADE的距离等于点O到平面ADE的距离为
 .或取A B的中点M.易证CM∥DA.点C到平面ADE的距离等于点M到平面ADE的距离为
.或取A B的中点M.易证CM∥DA.点C到平面ADE的距离等于点M到平面ADE的距离为 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
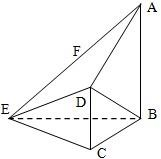 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.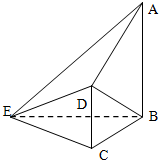 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.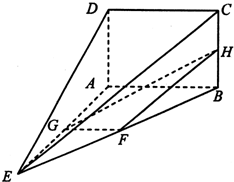 (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点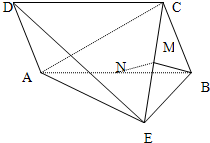 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.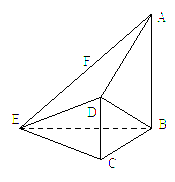 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,