题目内容
已知函数f(x)=(x+2)ln(x+1)-ax2-x(a∈R),g(x)=ln(x+1).
(1)若a=0,F(x)=f(x)-g(x),求函数F(x)的极值点及相应的极值.
(2)若对于任意x2>0,存在x1满足x1<x2且g(x1)=f(x2)成立,求a的取值范围.
(1)若a=0,F(x)=f(x)-g(x),求函数F(x)的极值点及相应的极值.
(2)若对于任意x2>0,存在x1满足x1<x2且g(x1)=f(x2)成立,求a的取值范围.
(1)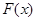 只有一个极小值点
只有一个极小值点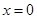 ,极小值为0. (2)
,极小值为0. (2)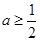
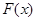 只有一个极小值点
只有一个极小值点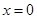 ,极小值为0. (2)
,极小值为0. (2)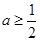
试题分析:(1)首先求出F(x)的表达式,然后求导
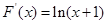 ,根据单数的性质,求出原函数的单调区间,即可求出函数F(x)的极值点及相应的极值.
,根据单数的性质,求出原函数的单调区间,即可求出函数F(x)的极值点及相应的极值.(2) 设
 ,依题意即求
,依题意即求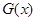 在
在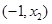 上存在零点时
上存在零点时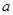 的取值范围.即只需要
的取值范围.即只需要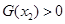 在
在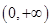 上恒成立.即
上恒成立.即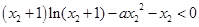 ,在
,在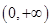 上恒成立.然后分
上恒成立.然后分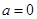 ,
,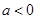 ,
,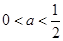 ,
,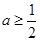 ,根据导数的性质分别求使
,根据导数的性质分别求使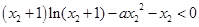 在
在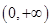 上成立的a的取值范围,最后求并集.
上成立的a的取值范围,最后求并集.试题解析:(1)
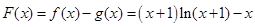 ,
,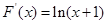 ,
,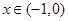
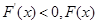 为减函数;
为减函数;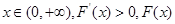 为增函数,
为增函数,所以
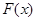 只有一个极小值点
只有一个极小值点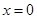 ,极小值为0. 4分
,极小值为0. 4分(2) 设
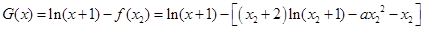
依题意即求
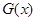 在
在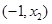 上存在零点时
上存在零点时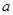 的取值范围.
的取值范围.又当
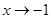 时,
时,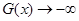 ,且
,且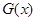 在定义域内单调递增,
在定义域内单调递增,所以只需要
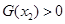 在
在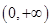 上恒成立.
上恒成立.即
 ,在
,在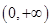 上恒成立.
上恒成立.即
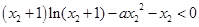 ,在
,在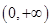 上恒成立. 7分
上恒成立. 7分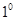 若
若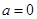 ,显然不成立,因为由第一问知
,显然不成立,因为由第一问知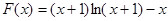 在
在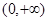 为增函数,
为增函数,故
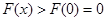
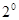
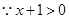 ,即
,即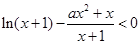 在
在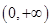 恒成立,
恒成立,不妨设
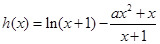 ,
,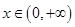
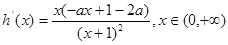 ,
,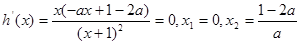 , 9分
, 9分若
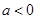 ,则
,则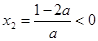 ,若
,若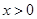 ,
,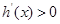 ,所以
,所以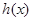 为增函数,
为增函数,
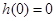 (不合题意),
(不合题意),若
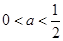 ,若
,若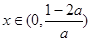 ,
,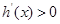 ,
,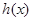 为增函数,
为增函数,
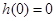 (不合题意),
(不合题意),若
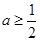 ,若
,若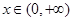 ,
,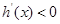 ,
,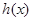 为减函数,
为减函数,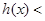
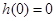 (符合题意),
(符合题意),综上所述,若
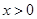 时,
时,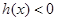
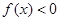 恒成立,
恒成立,则
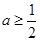 . 12分
. 12分
练习册系列答案
相关题目
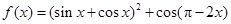 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;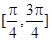 上的取值范围.
上的取值范围.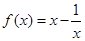 ,
, .
.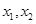 ,其中
,其中 ,求
,求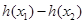 的最小值.
的最小值.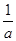 时,f
时,f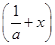 >f
>f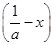 ;
;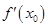 <0.
<0.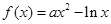 存在垂直于
存在垂直于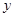 轴的切线,则实数
轴的切线,则实数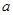 的取值范围是_______.
的取值范围是_______.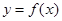 在
在 上为偶函数,当
上为偶函数,当 时,
时,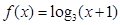 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是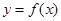 的定义域为
的定义域为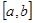 ,值域也是
,值域也是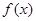 为“保域函数”,下列函数中是“保域函数”的有_____________.(填上所有正确答案的序号)
为“保域函数”,下列函数中是“保域函数”的有_____________.(填上所有正确答案的序号)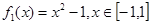 ;②
;②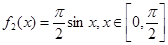 ;
; ;④
;④ ;
; .
. (a为常数).若
(a为常数).若 在区间[-1,+∞)上是增函数,则a的取值范围是( )
在区间[-1,+∞)上是增函数,则a的取值范围是( )