题目内容
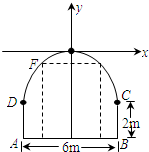
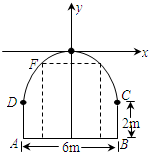一座拱桥桥洞的截面边界由抛物线弧段COD和矩形ABCD的三边组成，拱的顶部O距离水面5m，水面上的矩形的高度为2m，水面宽6m，如图所示，一艘船运载一个长方体形的集装箱，此箱平放在船上，已知船宽5m，船面距离水面1.5m，集装箱的尺寸为长×宽×高=4×3×3（m）．试问此船能否通过此桥？并说明理由．
解：设抛物线弧段COD的方程为y=ax2，由题意得C（3，-3），
∴-3=9a，∴a=-
∴y=-x2，
当x=2时，
，此时该点距水面5-
=
＜3+1.5
∴此船不能通过此桥
分析：根据抛物线特点设出二次函数解析式，把C坐标代入即可求得解析式，求出x=2时的点距水面的距离，即可得到结论．
点评：本题考查抛物线模型的构建，考查利用数学知识解决实际问题，确定抛物线的解析式是关键．
∴-3=9a，∴a=-
∴y=-
x2，当x=2时，
，此时该点距水面5-=＜3+1.5∴此船不能通过此桥
分析：根据抛物线特点设出二次函数解析式，把C坐标代入即可求得解析式，求出x=2时的点距水面的距离，即可得到结论．
点评：本题考查抛物线模型的构建，考查利用数学知识解决实际问题，确定抛物线的解析式是关键．
练习册系列答案
相关题目
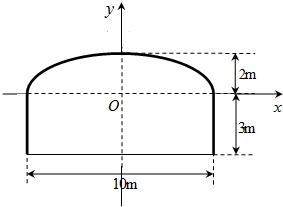一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成，如图所示．一辆卡车运载一个长方形的集装箱，此箱平放在车上与车同宽，车与箱的高度共计4.2米，箱宽3米，若要求通过隧道时，车体不得超过中线．试问这辆卡车是否能通过此隧道，请说明理由．
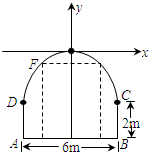一座拱桥桥洞的截面边界由抛物线弧段COD和矩形ABCD的三边组成，拱的顶部O距离水面5m，水面上的矩形的高度为2m，水面宽6m，如图所示，一艘船运载一个长方体形的集装箱，此箱平放在船上，已知船宽5m，船面距离水面1.5m，集装箱的尺寸为长×宽×高=4×3×3（m）．试问此船能否通过此桥？并说明理由．
