题目内容
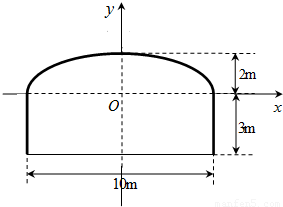
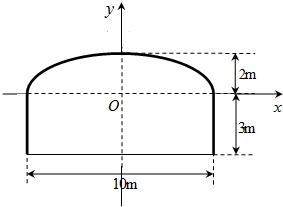一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成，如图所示．一辆卡车运载一个长方形的集装箱，此箱平放在车上与车同宽，车与箱的高度共计4.2米，箱宽3米，若要求通过隧道时，车体不得超过中线．试问这辆卡车是否能通过此隧道，请说明理由．
分析：建立如图所示的坐标系，则此隧道横截面的椭圆上半部分方程为：
+
=1，y≥0．令x=3，代入椭圆方程，解得y=1.6，由此知卡车能够通过此隧道．
| x2 |
| 25 |
| y2 |
| 4 |
解答：解：建立如图所示的坐标系，
则此隧道横截面的椭圆上半部分
方程为：
+
=1，y≥0．
令x=3，则代入椭圆方程，
解得y=1.6，因为1.6+3=4.6＞4.2，
所以，卡车能够通过此隧道．
解：建立如图所示的坐标系，则此隧道横截面的椭圆上半部分
方程为：
| x2 |
| 25 |
| y2 |
| 4 |
令x=3，则代入椭圆方程，
解得y=1.6，因为1.6+3=4.6＞4.2，
所以，卡车能够通过此隧道．
点评：本题考查椭圆的性质和应用，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成，如图所示．一辆卡车运载一个长方形的集装箱，此箱平放在车上与车同宽，车与箱的高度共计4.2米，箱宽3米，若要求通过隧道时，车体不得超过中线．试问这辆卡车是否能通过此隧道，请说明理由．
