题目内容
(12分) 一座拱桥桥洞的截面边界由抛物线弧段COD和矩形ABCD的三边组成,拱的顶部O距离水面5m,水面上的矩形的高度为2m,水面宽6m,如图所示,一艘船运载一个长方体形的集装箱,此箱平放在船上,已知船宽5m,船面距离水面1.5m,集装箱的尺寸为长×宽×高=4×3×3(m). 试问此船能否通过此桥?并说明理由.

(12分) 解:建立如图所示的坐标系,使抛物线顶点O在坐标原点,对称轴与y轴重合,
设抛物线方程为x2=ay (a<0) …………………………………………………… 2分
由题设条件知C(3,-3)在抛物线上, ∴9=-3a, a=-3,
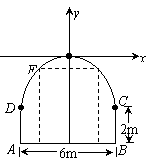 即抛物线方程为x2=-3y. ………………………………………………… 5分
即抛物线方程为x2=-3y. ………………………………………………… 5分
要使船能顺利通过,应使集装箱最高处E、F关于y轴对称.
于是设F(1.5, y0),则1.52=-3y0. ……………… 8分
∴y0=-0.75 此时点F距离水面的高度为5-0.75=4.25.
而集装箱高加船高为3+1.5=4.5>4.25,故此船不能通过此桥 …………… 12分

练习册系列答案
相关题目
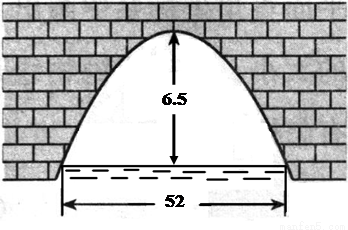
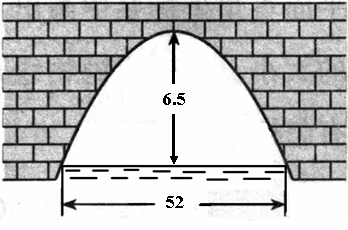
 米,拱顶离水平面
米,拱顶离水平面 米,水面上有一竹排上放有宽10米、高6米的木箱,问其能否安全通过拱桥?
米,水面上有一竹排上放有宽10米、高6米的木箱,问其能否安全通过拱桥?