题目内容
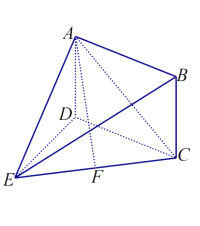
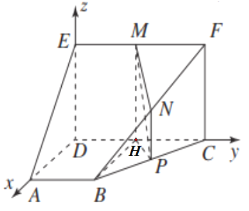
【题目】如图所示的多面体的底面![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为矩形,且
为矩形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)答案见解析.(2)![]()
【解析】
(1)先证明![]() 平面
平面![]() ,可得
,可得![]() ,取
,取![]() 中点
中点![]() ,利用等腰三角形的性质可得
,利用等腰三角形的性质可得![]() ,由线面垂直的判定即可得证;
,由线面垂直的判定即可得证;
(2)建立空间直角坐标系,求出各点坐标后,再求出平面![]() 的一个法向量
的一个法向量![]() 和直线
和直线![]() 的方向向量
的方向向量![]() ,求出两向量夹角的余弦值后利用平方关系即可得解.
,求出两向量夹角的余弦值后利用平方关系即可得解.
(1)证明:![]()
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]()
![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,![]()
![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]() 点
点![]() ,
,![]() ,
,![]() ,
,![]() 同在平面
同在平面![]() 内.
内.
在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
![]()
![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() 三条直线两两垂直且交于点
三条直线两两垂直且交于点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
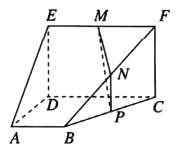
,![]() 轴,建立空间直角坐标系,如图.
轴,建立空间直角坐标系,如图.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,可得
中点,可得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则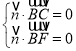 ,即
,即![]() ,
,
令![]() ,可得
,可得![]() ,
,![]() ,
,![]()
![]() ,
,
所以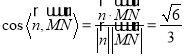 .
.
所以![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为 .
.

 阅读快车系列答案
阅读快车系列答案【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
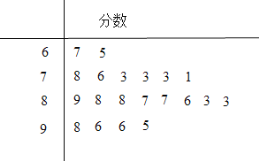
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: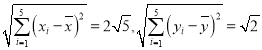
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: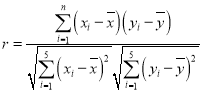 ,
,
参考数据:![]()