题目内容
17．设随机变量X的概率分布列为| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | a | $\frac{1}{4}$ | $\frac{1}{6}$ |
分析 本题中因为a是未知的，所以先根据随机变量取各个值的概率之和等于1求出a的值，然后根据P（|X-3|=1）=P（X=2，或X=4）进行计算．
解答 解：∵随机变量取各个值的概率之和等于1∴a=1-（$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{6}$）=$\frac{1}{4}$
∴P（|X-3|=1）=P（X=2，或X=4）=$\frac{1}{4}$$+\frac{1}{6}$=$\frac{5}{12}$．
点评 本题考查了随机变量取各个值的概率之和等于1，互斥事件的概率公式，属于基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
一张长方形纸片ABCD，AB=8cm，AD=6cm，将纸片沿着一条直线折叠，折痕（线段MN）将纸片分成两部分，面积分别为S1 cm2，S2 cm2，（S1≤S2）其中点A在面积为S1的部分内．记折痕长为lcm．
政府向市民宣传绿色出行（即乘公共汽车、地铁或步行出行），并进行广泛动员，三个月后，统计部门在一个小区随机抽取了100户家庭，调查了他们在政府动员后三个月的月平均绿色出行次数（单位：次），将所得数据分组，画出频率分布直方图（如图所示）．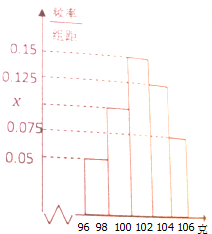
某工厂从一批产品中随机抽取40件进行检测，如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106）．