题目内容
【题目】已知![]() 为抛物线
为抛物线![]() :
: ![]() 的焦点,过点
的焦点,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 交
交![]() 于不同的两点
于不同的两点![]() ,直线
,直线![]() 交
交![]() 于不同的两点
于不同的两点![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设线段![]() 的中点分别为点
的中点分别为点![]() ,求证:
,求证: ![]() 为钝角.
为钝角.
【答案】(1){k|-![]() <k<0或k>2}(2)见解析
<k<0或k>2}(2)见解析
【解析】试题分析:
(1)由题意可设直线m的方程为y=k(x-2),将其代入抛物线方程后可得到一二次方程,根据判别式大于零可得k<0,或k>2.同理设直线n的方程为y=t(x-2),可得t<0,或t>2.根据以kt=-1,可解得k>0或-![]() <k<0,从而可得所求范围.(2)由(1)可得点M(2k,2k2-2k),N(2t,2t2-2t),根据F(0,1)可得到
<k<0,从而可得所求范围.(2)由(1)可得点M(2k,2k2-2k),N(2t,2t2-2t),根据F(0,1)可得到![]() 的坐标,通过证明
的坐标,通过证明![]() 且
且![]() 不共线可得
不共线可得![]() 为钝角.
为钝角.
试题解析:
(1)由题可知k≠0,设直线m的方程为y=k(x-2),
由![]() 消去y整理得x2-4kx+8k=0,①
消去y整理得x2-4kx+8k=0,①
因为直线直线m交![]() 于不同的两点
于不同的两点![]() ,
,
所以Δ=16k2-32k>0,
解得k<0,或k>2.
设直线n的方程为y=t(x-2),
由![]() 消去y整理得x2-4tx+8t=0,
消去y整理得x2-4tx+8t=0,
同理由Δ>0可得t<0,或t>2.
因为m⊥n,
所以kt=-1,
得-![]() ,或-
,或-![]() ,
,
解得k>0或-![]() <k<0.
<k<0.
故k的取值范围为{k|-![]() <k<0或k>2}.
<k<0或k>2}.
(Ⅱ)设A(x1,y1),B(x2,y2),M(x0,y0).
由①得x1+x2=4k,
所以![]() ,
,
故![]() ,
,
所以点M(2k,2k2-2k).
同理可得N(2t,2t2-2t),
又F(0,1),
所以![]() =(2k,2k2-2k-1),
=(2k,2k2-2k-1), ![]() =(2t,2t2-2t-1),
=(2t,2t2-2t-1),
![]() =4kt+(2k2-2k-1)(2t2-2t-1),
=4kt+(2k2-2k-1)(2t2-2t-1),
将kt=-1代入上式可得,
![]() =-2k2-2t2+6(k+t)-3=-2(k+t)2+6(k+t)-7=-2(k+t-
=-2k2-2t2+6(k+t)-3=-2(k+t)2+6(k+t)-7=-2(k+t-![]() )2-
)2-![]() <0
<0
因为2k(2t2-2t-1)-2t(2k2-2k-1)=2(![]() +k)≠0,
+k)≠0,
所以![]() 与
与![]() 不共线.
不共线.
所以可得∠MFN为钝角.

【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附: 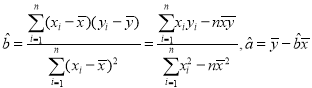 .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?