题目内容
在长方体ABCD-A1B1C1D1中，B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°，则异面直线B1C和C1D所成的角的余弦值为 ．
【答案】分析：设B1B=a，B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°推知BC=a，DC=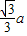
推知表示出长方体从一个顶点出发的三条棱的长度推知面对角线的长度，再用余弦定理求解．
解答：解：设B1B=a，
∵B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°
∴BC=a，DC=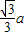
∴
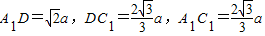
由余弦定理得：cos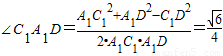
故答案为：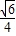
点评：本题主要考查异面直线所角的基本求法，若所成的角在直角三角形中，则用三角函数的定义，若在一般三角形中则用余弦定理．
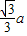推知表示出长方体从一个顶点出发的三条棱的长度推知面对角线的长度，再用余弦定理求解．解答：解：设B1B=a，
∵B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°
∴BC=a，DC=
∴
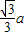
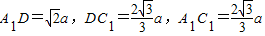
由余弦定理得：cos
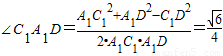
故答案为：
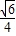
点评：本题主要考查异面直线所角的基本求法，若所成的角在直角三角形中，则用三角函数的定义，若在一般三角形中则用余弦定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在长方体ABCD-A'B'C'D'中，AB=
如图，在长方体ABCD-A′B′C′D′中，用截面截下一个棱锥C-A′DD′，求棱锥C-A′DD′的体积与剩余部分的体积之比．
（2013•上海） 如图，在长方体ABCD-A′B′C′D′中，AB=2，AD=1，AA′=1．证明直线BC′平行于平面D′AC，并求直线BC′到平面D′AC的距离．
（2009•青浦区二模）（理）在长方体ABCD-A'B'C'D'中，AB=2，AD=1，AA'=1．
已知在长方体ABCD-A′B′C′D′中，点E为棱CC′上任意一点，AB=BC=2，CC′=1．