题目内容
【题目】设复数![]() ,其中xnyn∈R,n∈N*,i为虚数单位,
,其中xnyn∈R,n∈N*,i为虚数单位,![]() ,z1=3+4i,复数zn在复平面上对应的点为Zn.
,z1=3+4i,复数zn在复平面上对应的点为Zn.
(1)求复数z2,z3,z4的值;
(2)是否存在正整数n使得![]() ?若存在,求出所有满足条件的
?若存在,求出所有满足条件的![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)求数列![]() 的前
的前![]() 项之和.
项之和.
【答案】(1)z2=﹣1+7i,z3=﹣8+6i,z4=﹣14﹣2i;(2)存在,n=4k+1,k∈N;(3)1+2102
【解析】
(1)利用已知条件之间求解z2,z3,z4;
(2)求出![]() ,利用复数的幂运算,求解即可;
,利用复数的幂运算,求解即可;
(3)通过![]() ,推出xn+4=﹣4xn,yn+4=﹣4yn,得到xn+4yn+4=16xnyn,然后求解数列的和即可.
,推出xn+4=﹣4xn,yn+4=﹣4yn,得到xn+4yn+4=16xnyn,然后求解数列的和即可.
(1)z2=(1+i)(3+4i)=﹣1+7i,![]() ,
,![]() .
.
(2)若![]() ,则存在实数λ,使得
,则存在实数λ,使得![]() ,故
,故![]() ,
,
即(xn,yn)=λ(x1,y1),
又zn+1=(1+i)zn,故![]() ,即
,即![]() 为实数,
为实数,
![]() ,
,![]() ,故n﹣1为4的倍数,即n﹣1=4k,n=4k+1,k∈N;
,故n﹣1为4的倍数,即n﹣1=4k,n=4k+1,k∈N;
(3)因为![]() ,故xn+4=﹣4xn,yn+4=﹣4yn,所以xn+4yn+4=16xnyn,
,故xn+4=﹣4xn,yn+4=﹣4yn,所以xn+4yn+4=16xnyn,
又x1y1=12,x2y2=﹣7,x3y3=﹣48,x4y4=28,
x1y1+x2y2+x3y3+…+x100y100
=(x1y1+x2y2+x3y3+x4y4)+(x5y5+x6y6+x7y7+x8y8)+…+(x97y97+x98y98+x99y99+x100y100)
=![]() ,
,
而![]() ,
,![]() ,
,
所以数列{xnyn}的前102项之和为1﹣2100+12×2100﹣7×2100=1+2102.

 阅读快车系列答案
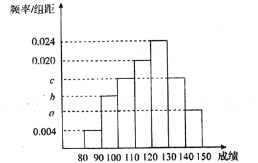
阅读快车系列答案【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从数学成绩为“优”的同学中随机抽取2人,求两人恰好均为物理成绩“优”的概率.
【题目】北京联合张家口获得2022年第24届冬奥会举办权,我国各地掀起了发展冰雪运动的热潮,现对某高中的学生对于冰雪运动是否感兴趣进行调查,该高中男生人数是女生的1.2倍,按照分层抽样的方法,从中抽取110人,调查高中生“是否对冰雪运动感兴趣”得到如下列联表:
感兴趣 | 不感兴趣 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 110 |
(1)补充完成上述![]() 列联表;
列联表;
(2)是否有99%的把握认为是否喜爱冰雪运动与性别有关.
附:![]() (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】某学习小组在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是小组成员在3月份的31天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月2日 | 3月8日 | 3月15日 | 3月22日 | 3月28日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 14 |
(1)在这个学习小组中负责统计数据的那位同学为了减少计算量,他从这5天中去掉了3月2日与3月28日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所去掉的试验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: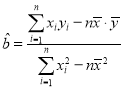 ,
,![]() )(参考数据:
)(参考数据:![]() ,
,![]() )
)