题目内容
下列说法中
① 若定义在R上的函数 满足
满足 ,则6为函数
,则6为函数 的周期;
的周期;
② 若对于任意 ,不等式
,不等式 恒成立,则
恒成立,则 ;
;
③ 定义:“若函数 对于任意
对于任意 R,都存在正常数
R,都存在正常数 ,使
,使 恒成立,则称函数
恒成立,则称函数 为有界泛函.”由该定义可知,函数
为有界泛函.”由该定义可知,函数 为有界泛函;
为有界泛函;
④对于函数 设
设 ,
, ,…,
,…, (
( 且
且 ),令集合
),令集合 ,则集合
,则集合 为空集.正确的个数为
为空集.正确的个数为
| A.1个 | B.2个 | C.3个 | D.4个 |
B
解析试题分析:① 因为 ,所以
,所以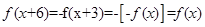 ,所以函数的周期为6。所以若定义在R上的函数
,所以函数的周期为6。所以若定义在R上的函数 满足
满足 ,则6为函数
,则6为函数 的周期,正确;
的周期,正确;
② 若对于任意 ,不等式
,不等式 恒成立,
恒成立,
即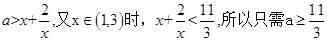 。所以错误;
。所以错误;
③若命题成立,则必有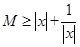 ,x∈R恒成立,这是不可能的,故不对;
,x∈R恒成立,这是不可能的,故不对;
④对于函数 易知
易知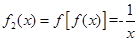 ,
, ,
,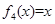 ,
,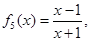 ……,故
……,故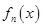 的值是以4为周期重复出现的,所以
的值是以4为周期重复出现的,所以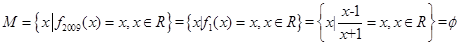 ,则集合
,则集合 为空集.,正确。
为空集.,正确。
考点:函数的周期性;二次函数的性质;空集的性质。
点评:本题主要考查函数的周期,恒成立求参数,利用周期性求值,新定义函数的正确性验证,本题作为一个选择题运算量大,且变形技巧性强,实为得分不易之题.

练习册系列答案
相关题目
函数 +1(a>0,a≠1)的图象必经过定点 ( )
+1(a>0,a≠1)的图象必经过定点 ( )
| A.(0,1) | B.(2,1) | C.(2,2) | D.(2,3) |
下列函数是偶函数,且在 上单调递减的是 ( )
上单调递减的是 ( )
A. | B. | C. | D. |
若a是函数 的零点,若
的零点,若 ,则
,则 的值满足
的值满足
A. | B. | C. | D. 的符号不确定 的符号不确定 |
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |

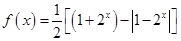 的图象大致为 ( )
的图象大致为 ( )
 的图象的大致形状是
的图象的大致形状是 
 和
和 ,定义运算“
,定义运算“ ”:
”: .设函数
.设函数 ,
, .若函数
.若函数 的图象与
的图象与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数 的取值范围是( )
的取值范围是( )


