题目内容
若复数z满足|z+1|+|z-1|=2,则|z+i-1|的最小值是
1
1
.分析:根据题意可得满足|z+1|+|z-1|=2的点Z几何意义为线段AB,进而分析|z+i-1|的几何意义,根据图象法可得答案.
解答: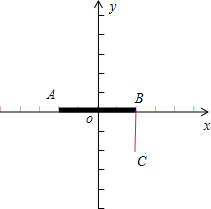 解:复数z满足|z+1|+|z-1|=2,
解:复数z满足|z+1|+|z-1|=2,
则复数Z表示的点到(-1,0),(1,0)两点的距离之和为2,
而(-1,0),(1,0)两点间的距离为2,
设A为(-1,0),B(1,0),
则Z表示的点的集合为线段AB,
|z+i-1|的几何意义为点Z到点C(1,-1)的距离,
分析可得,Z在点(1,0)时,
|z+i-1|取得最小值,且其最小值为1.
故答案为1.
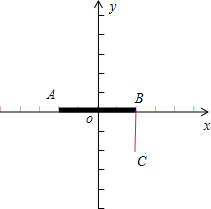 解:复数z满足|z+1|+|z-1|=2,
解:复数z满足|z+1|+|z-1|=2,则复数Z表示的点到(-1,0),(1,0)两点的距离之和为2,
而(-1,0),(1,0)两点间的距离为2,
设A为(-1,0),B(1,0),
则Z表示的点的集合为线段AB,
|z+i-1|的几何意义为点Z到点C(1,-1)的距离,
分析可得,Z在点(1,0)时,
|z+i-1|取得最小值,且其最小值为1.
故答案为1.
点评:本题考查复数的模的计算、复数的代数表示法及其几何意义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目