题目内容
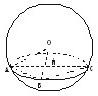
已知球面上的三点A、B、C,AB=6,BC=8,AC=10,球的半径为13,求球心到平面ABC的距离.
∵62+82=102,∴△ABC为Rt△.
∵球心O在平面ABC内的射影M是截面圆的圆心,
∴M是AC的中点且OM⊥AC.
在Rt△OAM中,OM=
=12.
∴球心到平面ABC的距离为12.
∵球心O在平面ABC内的射影M是截面圆的圆心,
∴M是AC的中点且OM⊥AC.
在Rt△OAM中,OM=
| OA2-AM2 |
∴球心到平面ABC的距离为12.


练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目