题目内容
【题目】下列四个图形中,正方体棱上的四个中点共面的图形是( ).

A.甲与乙B.乙与丙C.丙与丁D.丁与甲
【答案】A
【解析】
如图所示:利用空间点线面位置关系可以证明图中中点E、F、G、H、M、N六点共面,进而判断甲乙图中对应的四点为分别为:H、F、G、N和E、F、G、M均在平面EFGNMH内,所以可得甲乙图形符合要求;然后可判断丙和丁图中对应的四点不共面.
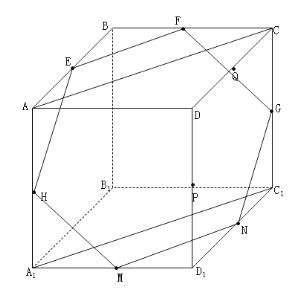
如图所示, E、F、G、H、M、N、P、Q均为正方体AC1棱上的中点,所以有:EF![]() AC,MN
AC,MN![]() A1C1,AC
A1C1,AC![]() A1C1,得EF
A1C1,得EF![]() MN,所以得EF、MN可确定一个平面α,同理EH、NG可确定一个平面β,又因为E、F、M三点不共线只能确定一个平面,所以α、β重合,即E、F、G、H、M、N六点共面为平面EN,所以有:
MN,所以得EF、MN可确定一个平面α,同理EH、NG可确定一个平面β,又因为E、F、M三点不共线只能确定一个平面,所以α、β重合,即E、F、G、H、M、N六点共面为平面EN,所以有:
甲图中对应的四点为H、F、G、N在平面EN内即共面;
乙图中对应的四点为E、F、G、M在平面EN内即共面;
丙图中对应的四点为E、F、P、M其中P点不在平面EN内即得四点不共面;
丁图中对应的四点为E、H、G、Q其中Q点不在平面EN内即得四点不共面;
综上可得甲乙图满足要求.
故选:A

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目