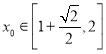题目内容
【题目】已知圆C:x2+(y-a)2=4,点A(1,0).
(1)当过点A的圆C的切线存在时,求实数a的取值范围;
(2)设AM、AN为圆C的两条切线,M、N为切点,当MN=![]() 时,求MN所在直线的方程.
时,求MN所在直线的方程.
【答案】(1)a≥![]() 或a≤-
或a≤-![]() .(2)x-2y=0或x+2y=0.
.(2)x-2y=0或x+2y=0.
【解析】试题分析:(1)由直线与圆的位置关系,得当点A在圆外或圆上过点A的圆C的切线存在.再由点与圆的位置关系,建立关于a的不等式,解之即得实数a的取值范围;
(2)根据圆的对称性得到|DM|=![]() |MN|=
|MN|=![]() .利用垂径定理算出CD的长度,在Rt△MCD中,算出cos∠MCD的值,得cos∠MCA=
.利用垂径定理算出CD的长度,在Rt△MCD中,算出cos∠MCD的值,得cos∠MCA=![]() .然后在Rt△MCA中利用解三角形知识算出AC长,结合|OC|=2得出|AM|=1.由题意知MN是以A为圆心、半径为AM的圆与圆C的公共弦,由此列式即可求出MN所在直线的方程.
.然后在Rt△MCA中利用解三角形知识算出AC长,结合|OC|=2得出|AM|=1.由题意知MN是以A为圆心、半径为AM的圆与圆C的公共弦,由此列式即可求出MN所在直线的方程.
试题解析:(1)过点A的切线存在,即点A在圆外或圆上,
∴1+a2≥4,∴a≥![]() 或a≤-
或a≤-![]() .
.
(2)设MN与AC交于点D,O为坐标原点.
∵MN=![]() ,∴DM=
,∴DM=![]() .
.
又MC=2,∴CD=![]() =
=![]() ,
,
∴cos∠MCA=![]() =
=![]()
∵AC=![]() =
=![]() ,∴OC=2,AM=1,
,∴OC=2,AM=1,
MN是以点A为圆心,半径AM=1的圆A与圆C的公共弦,圆A的方程为(x-1)2+y2=1
圆C的方程为x2+(y-2)2=4,或x2+(y+2)2=4,
∴MN所在直线的方程为:(x-1)2+y2-1-x2-(y-2)2+4=0,
即x-2y=0或(x-1)2+y2-1-x2-(y+2)2+4=0,
即x+2y=0,因此,MN所在直线的方程为x-2y=0或x+2y=0.

 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】在某批次的某种灯泡中,随机地抽取![]() 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命(天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(Ⅰ)根据频率分布表中的数据,写出![]() ,
, ![]() 的值.
的值.
(Ⅱ)某人从灯泡样品中随机地购买了![]() 个,求
个,求![]() 个灯泡中恰有一个是优等品的概率.
个灯泡中恰有一个是优等品的概率.
(Ⅲ)某人从这个批次的灯泡中随机地购买了![]() 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用![]() 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.