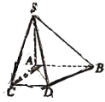
题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() 分别为
分别为![]() 中点,且
中点,且![]() ,
,![]() .
.
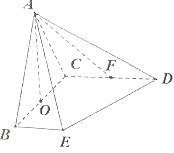
(1)![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)求四棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连结![]() ,利用勾股定理逆定理可证明
,利用勾股定理逆定理可证明![]() ,又易证
,又易证![]() ,可证明
,可证明![]() 平面
平面![]() (2)连接
(2)连接![]() ,根据
,根据![]() ,
,![]() 平面
平面![]() 可得
可得![]() ,进而
,进而![]() ,利用
,利用![]() 为
为![]() 中点可得结论(3)OA是棱锥的高,求底面直角梯形
中点可得结论(3)OA是棱锥的高,求底面直角梯形![]() 的面积即可代入体积公式计算.
的面积即可代入体积公式计算.
(1)证明:连结![]()
![]() ,
,![]() 为
为![]() 的中点
的中点
![]() ,且
,且![]() ,
,![]()
又![]() ,
,![]() 是
是![]() 中点,
中点,![]() ,
,
![]()
由已知![]() ,
,![]()
![]() ,且
,且![]() 是平面
是平面![]() 内两条相交直线
内两条相交直线
![]() 平面
平面![]() .
.
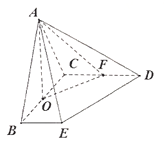
(2)连接![]() ,由已知底面
,由已知底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]()
则四边形![]() 为平行四边形
为平行四边形
所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
所以![]()
因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点
中点
所以![]() ,又因为点
,又因为点![]() 为
为![]() 的中点.
的中点.
所以![]() .
.
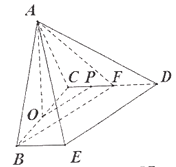
(3)由(1)![]() 平面
平面![]() 得
得![]() 为四棱锥
为四棱锥![]() 的高,且
的高,且![]()
又因为![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,
所以直角梯形![]() 的面积为
的面积为![]()
则四棱锥![]() 的体积
的体积![]()

【题目】在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生
男生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表二:女生
女生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)求![]() ,
,![]() 的值;
的值;
(2)从表二的非优秀学生中随机抽取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(3)由表中统计数据填写![]() 列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 | 45 |
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.01 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
【题目】市政府为了节约用水,调查了100位居民某年的月均用水量(单位:![]() ),频数分布如下:
),频数分布如下:
分组 |
|
|
|
|
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根据所给数据将频率分布直图补充完整(不必说明理由);
(2)根据频率分布直方图估计本市居民月均用水量的中位数;
(3)根据频率分布直方图估计本市居民月均用水量的平均数(同一组数据由该组区间的中点值作为代表).