题目内容
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
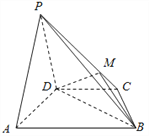
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)设![]() ,由中位线定理证得
,由中位线定理证得![]() 平面
平面![]() ;(2)由
;(2)由![]() 平面
平面![]() 平面
平面![]() 平
平![]() .
.
试题解析:(1)设AC∩BD=H,连接MH,
∵H为平行四边形ABCD对角线的交点,∴H为AC中点,
又∵M为PC中点,∴MH为△PAC中位线,
可得MH∥PA,
MH平面MBD,PA平面MBD,
所以PA∥平面MBD.
(2)∵PD⊥平面ABCD,AD平面ABCD,
∴PD⊥AD,
又∵AD⊥PB,PD∩PB=D,
∴AD⊥平面PDB,结合BD平面PDB,得AD⊥BD
∵PD⊥BD,且PD、AD是平面PAD内的相交直线
∴BD⊥平面PAD.

练习册系列答案
相关题目
【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。