Question

【题目】已知数列（）的通项公式为（）.

（1）分别求的二项展开式中的二项式系数之和与系数之和；

（2）求的二项展开式中的系数最大的项；

（3）记（），求集合的元素个数（写出具体的表达式）.

Answer 1

【答案】（1），0；（2），；（3）.

【解析】

（1）根据二项展开式直接得二项式系数之和为，利用赋值法求二项展开式中的系数之和；

（2）根据二项展开式通项公式得系数，再列方程组解得系数最大的项；

（3）先根据二项式定理将展开成整数与小数，再根据奇偶性分类讨论元素个数，最后根据符号数列合并通项.

（1）二项展开式中的二项式系数之和为，

令得二项展开式中的系数之和为；

（2）

设二项展开式中的系数最大的项数为

则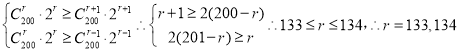

因此二项展开式中的系数最大的项为，

（3）

所以当为偶数时，集合的元素个数为

当为奇数时，集合的元素个数为

综上，元素个数为