题目内容
4．
如图，已知P是矩形ABCD所在平面外一点，PA⊥平面ABCD，E、F分别是AB，PC的中点．若∠PDA=45°，则EF与平面ABCD所成角的大小是（ ）| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
分析 取PD的中点为G，过G作GH⊥AD，垂足为H，则可得∠GAH为AG与平面ABCD所成的角，即为所求角，求解即可．
解答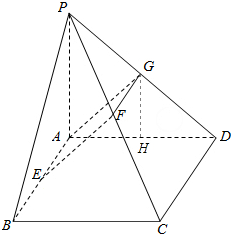 
解：取PD中点G，连接AG、FG，
∵EF分别为AB、PC的中点，
∴AE=$\frac{1}{2}$AB，GF∥DC且GF=$\frac{1}{2}$DC，
又在矩形ABCD中AB∥CD且AB=CD，
∴AE∥GF且AE=GF，
∴四边形AEFG是平行四边形，
∴AG∥EF，
∴AG与平面ABCD所成的角等于EF与平面ABCD所成的角，
过G作GH⊥AD，垂足为H，则GH∥PA
∵PA⊥平面ABCD，∴GH⊥平面ABCD，
∴∠GAH为AG与平面ABCD所成的角，即为所求角，
∵∠PDA=45°，G为PD的中点，
∴∠GAH=45°，
即EF与平面ABCD所成的角为45°．
故选：C．
点评 本题考查线面角，熟练掌握判定定理内容、正确找出线面角是关键．
练习册系列答案
相关题目
16．已知函数$f（x）=\left\{\begin{array}{l}-{x^2}+2x，x≤0\\ ln（x+1），x＞0\end{array}\right.$，若|f（x）|≥2ax，则a的取值范围是（ ）
| A． | （-∞，0] | B． | [-2，1] | C． | [-2，0] | D． | [-1，0] |
已知正三棱柱ABC-A1B1C1中，AB=AA1，O，D，E分别是AB，A1B1，AA1的中点，点F是AB边上靠近A的四等分点．证明：
9．
如图，网格纸上小正方形的边长为1，粗线是一个棱锥的三视图，则此棱锥的体积为（ ）
如图，网格纸上小正方形的边长为1，粗线是一个棱锥的三视图，则此棱锥的体积为（ ）| A． | $\frac{{4\sqrt{2}}}{3}$ | B． | $\frac{8}{3}$ | C． | $\frac{{8\sqrt{2}}}{3}$ | D． | 8 |
16．函数 f（x）=cos3x+sin2x-cosx的最大值是（ ）
| A． | $\frac{8}{27}$ | B． | 1 | C． | $\frac{32}{27}$ | D． | 2 |
13．已知直线l⊥平面α，直线m?平面β，给出下列命题：
（1）α∥β⇒l⊥m，（2）α⊥β⇒l∥m，（3）l∥m⇒α⊥β，（4）l⊥m⇒α⊥β，
其中正确的是（ ）
（1）α∥β⇒l⊥m，（2）α⊥β⇒l∥m，（3）l∥m⇒α⊥β，（4）l⊥m⇒α⊥β，
其中正确的是（ ）
| A． | （1）（2）（3） | B． | （2）（3）（4） | C． | （2）（4） | D． | （1）（3） |
如图，梯形ABCD中，DC∥AB，AD=DC=CB=2，AB=4，矩形AEFC中，AE=$\sqrt{3}$，平面AEFC⊥平面ABCD，点G是线段EF的中点．