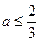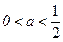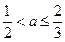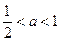题目内容
设P:函数y=ax2-2x+1在[1,+∞)内单调递减,Q:曲线y=x2-2ax+4a+5与x轴没有交点.如果P与Q有且只有一个正确,求a的 取值范围.
取值范围.
 取值范围.
取值范围.a≤-1或0< a<5
a<5
 a<5
a<5解:由P知,a=0或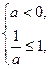 解得a≤0.由Q知Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.
解得a≤0.由Q知Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.
若P正确,Q不正确,则有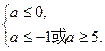 ∴a≤-1.
∴a≤-1.
若P不正确,Q正确,则有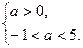 ∴0<a<5.
∴0<a<5.
综上可知,a的取值范围为a≤-1或0< a<5.
a<5.
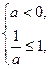 解得a≤0.由Q知Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.
解得a≤0.由Q知Δ=(-2a)2-4(4a+5)<0,解得-1<a<5.若P正确,Q不正确,则有
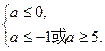 ∴a≤-1.
∴a≤-1.若P不正确,Q正确,则有
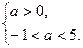 ∴0<a<5.
∴0<a<5.综上可知,a的取值范围为a≤-1或0<
 a<5.
a<5.
练习册系列答案
相关题目
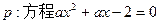 在[-1,1]上有解,
在[-1,1]上有解,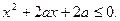
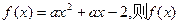 的图象必定过两定点,试写出这两定点的坐标.
的图象必定过两定点,试写出这两定点的坐标. 和
和 是一对异面直线,它们所成个的角为θ,且
是一对异面直线,它们所成个的角为θ,且 ,以下四个命题中,
,以下四个命题中, ,使
,使 ;
;  ;
;  的平面中存在平面
的平面中存在平面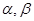 ,使它们所形成的二面角(较小的)的大小为
,使它们所形成的二面角(较小的)的大小为 ;
;  ,使
,使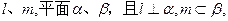 ,给出下列四个命题:
,给出下列四个命题: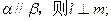 ②若
②若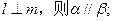 ③若
③若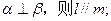
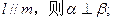 其中正确命题的个数是 ( )
其中正确命题的个数是 ( )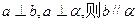
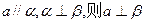
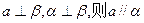
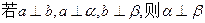
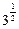 是有理数,则x是无理数”的逆否命题
是有理数,则x是无理数”的逆否命题 ④
④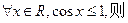 ( )
( )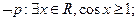
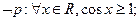

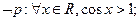
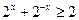
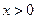 且
且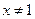 时,
时,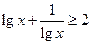
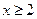 时,
时,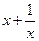 的最小值
的最小值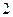
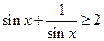
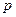 :关于
:关于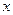 的函数
的函数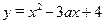 在
在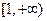 上是增函数,命题
上是增函数,命题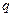 :函数
:函数 为减函数,若
为减函数,若 为真命题,则实数m的取值范围( )
为真命题,则实数m的取值范围( )