题目内容
200辆汽车通过某一段公路时，时速的频率分布直方图如右图所示，则时速在[50，70)的汽车大约有（ ）.
Ａ．60辆 B．80辆 Ｃ．70辆 Ｄ．140辆
D
解析试题分析：需根据直方图中求出各个矩形的面积，即为各组频率，再由总数乘以频率即得各组频数．解：由直方图可知，时速在[50，60]的频率为0.03×10=0.3 时速在[60，70]的频率为0.04×10=0.4 所以时速在[50，70]的汽车大约有200×（0.3+0.4）=140辆．故答案为D．
考点：直方图
点评：本题考查频率分布直方图的相关知识．直方图中的各个矩形的面积代表了频率，所以各个矩形面积之和为1．
练习册系列答案
计算高手系列答案
相关题目
两个相关变量满足如下关系：
| x | 10 | 15 | 20 | 25 | 30 |
| y | 1003 | 1005 | 1010 | 1011 | 1014 |
A.
＝0.56x＋997.4 B. ＝0.63x－231.2C.
＝50.2x＋501.4 D. ＝60.4x＋400.7 为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为 ( ) 
| A．0.27,78 | B．0.27,83 | C．2.7,78 | D．2.7,83 |
已知一个线性回归方程为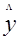
＝2x＋45，其中x的取值依次为1, 7, 5, 13, 19，
则
＝ ( )
| A．58.5 | B．46.5 | C．63 | D．75 |
下图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图，设
甲、乙两组数据的平均数分别为
，
，中位数分别为m甲，m乙，则
| A．<，m甲> m乙 | B．<，m甲< m乙 |
| C．，m甲> m乙 | D．>，m甲< m乙 |
下面有关抽样的描述中，错误的是（ ）
| A．在简单抽样中，某一个个体被抽中的可能性与第n次抽样有关，先抽到的可能性较大 |
| B．系统抽样又称为等距抽样，每个个体入样的可能性相等 |
| C．分层抽样为了保证每个个体入样的可能性相等必须每层等可能性抽样 |
| D．抽样的原则是“搅拌均匀”且“等可能地抽到每个个体” |
某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )
A． ＝－10x＋200 | B．＝10x＋200 |
| C．＝－10x－200 | D．＝10x－200 |
独立性检验，适用于检查
变量之间的关系（ ）
| A．线性 | B．非线性 | C．解释与预报 | D．分类 |