题目内容
为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( ) 
| A.0.27,78 | B.0.27,83 | C.2.7,78 | D.2.7,83 |
A
解析试题分析:由频率分布直方图知组矩为0.1,4.3~4.4间的频数为100×0.1×0.1=1.4.4~4.5间的频数为100×0.1×0.3=3.又前4组的频数成等比数列,∴公比为3.根据后6组频数成等差数列,且共有100-13=87人.从而4.6~4.7间的频数最大,且为1×33=27,∴a=0.27,设公差为d,则6×27+ d=87.∴d=-5,从而b=4×27+
d=87.∴d=-5,从而b=4×27+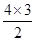 (-5)=78.故选:A.
(-5)=78.故选:A.
考点:本题考查了频率分布直方图的运用
点评:频率分布直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1,同时考查分析问题的能力,属于基础题.

 智趣寒假作业云南科技出版社系列答案
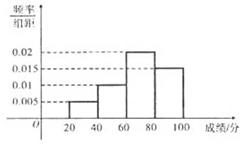
智趣寒假作业云南科技出版社系列答案某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为 ( )
| A.588 | B.480 | C.450 | D.120 |
两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是
| A.模型1的相关指数R2为0.96 | B.模型2的相关指数R2为0.86 |
| C.模型3的相关指数R2为0.73 | D.模型4的相关指数R2为0.66 |
甲、乙两位运动员在5场比赛的得分情况如茎叶图所示,记甲、乙两人的平均得分分别为 ,则下列判断正确的是
,则下列判断正确的是
A.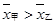 ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
B.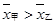 ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
C. ;甲比乙成绩稳定 ;甲比乙成绩稳定 |
D. ;乙比甲成绩稳定 ;乙比甲成绩稳定 |
下图是2013年某市举行的名师评选活动,七位评委为某位教师打出的分数的茎叶统计图,去掉一个最高分和一个最低分,所剩数据的平均数和方差分别为( )
| 7 | 9 | | | | |
| 8 | 4 | 4 | 6 | 4 | 7 |
| 9 | 3 | | | | |
B. 84,1.6
C. 85,1.6
D. 85,4
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
右表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是 ,则a等于( ).
,则a等于( ).
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 5.5 | 5 | 4 | 3.5 |

 若低于60分的人数是15人,则该班的学生人数是( )
若低于60分的人数是15人,则该班的学生人数是( )