题目内容
已知函数f(x)=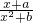 是定义在R上的奇函数,其值域为[-
是定义在R上的奇函数,其值域为[-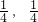 ].
].
(1)试求a、b的值;
(2)函数y=g(x)(x∈R)满足:①当x∈[0,3)时,g(x)=f(x);②g(x+3)=g(x)lnm(m≠1).
①求函数g(x)在x∈[3,9)上的解析式;
②若函数g(x)在x∈[0,+∞)上的值域是闭区间,试探求m的取值范围,并说明理由.
解:(1)由函数f(x)定义域为R,∴b>0.
又f(x)为奇函数,则f(-x)=-f(x)对x∈R恒成立,得a=0.
因为y=f(x)=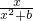 的定义域为R,所以方程yx2-x+by=0在R上有解.
的定义域为R,所以方程yx2-x+by=0在R上有解.
当y≠0时,由△≥0,得-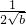 ≤y≤
≤y≤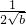 ,
,
而f(x)的值域为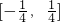 ,所以
,所以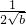 =
= ,解得b=4;
,解得b=4;
当y=0时,得x=0,可知b=4符合题意.所以b=4.
(2)①因为当x∈[0,3)时,g(x)=f(x)=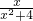 ,
,
所以当x∈[3,6)时,g(x)=g(x-3)lnm=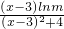 ;
;
当x∈[6,9)时,g(x)=g(x-6)(lnm)2=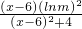 ,
,
故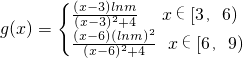
②因为当x∈[0,3)时,g(x)=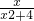 在x=2处取得最大值为
在x=2处取得最大值为 ,在x=0处取得最小值为0,
,在x=0处取得最小值为0,
所以当3n≤x<3n+3(n≥0,n∈Z)时,g(x)=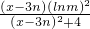 分别在x=3n+2和x=3n处取得最值为
分别在x=3n+2和x=3n处取得最值为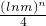 与0.
与0.
(ⅰ) 当|lnm|>1时,g(6n+2)=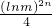 的值趋向无穷大,从而g(x)的值域不为闭区间;
的值趋向无穷大,从而g(x)的值域不为闭区间;
(ⅱ) 当lnm=1时,由g(x+3)=g(x)得g(x)是以3为周期的函数,从而g(x)的值域为闭区间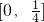 ;
;
(ⅲ) 当lnm=-1时,由g(x+3)=-g(x)得g(x+6)=g(x),得g(x)是以6为周期的函数,
且当x∈[3,6)时g(x)=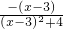 值域为
值域为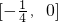 ,从而g(x)的值域为闭区间
,从而g(x)的值域为闭区间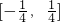 ;
;
(ⅳ) 当0<lnm<1时,由g(3n+2)=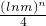 <
< ,得g(x)的值域为闭区间
,得g(x)的值域为闭区间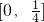 ;
;
(ⅴ) 当-1<lnm<0时,由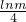 ≤g(3n+2)=
≤g(3n+2)=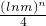 <
< ,从而g(x)的值域为闭区间
,从而g(x)的值域为闭区间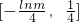 .
.
综上知,当m∈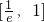 ∪(1,e],即0<lnm≤1或-1≤lnm<0时,g(x)的值域为闭区间.
∪(1,e],即0<lnm≤1或-1≤lnm<0时,g(x)的值域为闭区间.
分析:(1)由于 函数f(x)=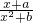 是定义在实数集R上的奇函数,则f(-x)=-f(x),构造方程,可求a与b值;
是定义在实数集R上的奇函数,则f(-x)=-f(x),构造方程,可求a与b值;
(2)由题意以及①当x∈[0,3)时,g(x)=f(x);②g(x+3)=g(x)lnm(m≠1).得到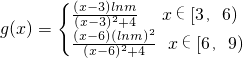 ;
;
对参数lnm分类讨论,再依据函数g(x)在x∈[0,+∞)上的值域是闭区间,即可得到m的取值范围.
点评:本题考查的知识点是函数奇偶性,函数的值域,解题的关键是熟练掌握函数奇偶性的性质,以及分类讨论求出参数的取值范围.
又f(x)为奇函数,则f(-x)=-f(x)对x∈R恒成立,得a=0.
因为y=f(x)=
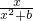 的定义域为R,所以方程yx2-x+by=0在R上有解.
的定义域为R,所以方程yx2-x+by=0在R上有解.当y≠0时,由△≥0,得-
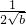 ≤y≤
≤y≤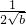 ,
,而f(x)的值域为
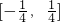 ,所以
,所以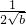 =
= ,解得b=4;
,解得b=4;当y=0时,得x=0,可知b=4符合题意.所以b=4.
(2)①因为当x∈[0,3)时,g(x)=f(x)=
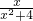 ,
,所以当x∈[3,6)时,g(x)=g(x-3)lnm=
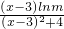 ;
;当x∈[6,9)时,g(x)=g(x-6)(lnm)2=
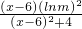 ,
,故
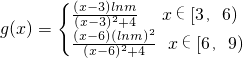
②因为当x∈[0,3)时,g(x)=
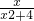 在x=2处取得最大值为
在x=2处取得最大值为 ,在x=0处取得最小值为0,
,在x=0处取得最小值为0,所以当3n≤x<3n+3(n≥0,n∈Z)时,g(x)=
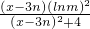 分别在x=3n+2和x=3n处取得最值为
分别在x=3n+2和x=3n处取得最值为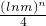 与0.
与0.(ⅰ) 当|lnm|>1时,g(6n+2)=
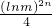 的值趋向无穷大,从而g(x)的值域不为闭区间;
的值趋向无穷大,从而g(x)的值域不为闭区间;(ⅱ) 当lnm=1时,由g(x+3)=g(x)得g(x)是以3为周期的函数,从而g(x)的值域为闭区间
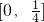 ;
;(ⅲ) 当lnm=-1时,由g(x+3)=-g(x)得g(x+6)=g(x),得g(x)是以6为周期的函数,
且当x∈[3,6)时g(x)=
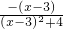 值域为
值域为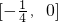 ,从而g(x)的值域为闭区间
,从而g(x)的值域为闭区间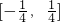 ;
;(ⅳ) 当0<lnm<1时,由g(3n+2)=
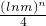 <
< ,得g(x)的值域为闭区间
,得g(x)的值域为闭区间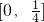 ;
;(ⅴ) 当-1<lnm<0时,由
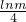 ≤g(3n+2)=
≤g(3n+2)=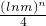 <
< ,从而g(x)的值域为闭区间
,从而g(x)的值域为闭区间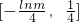 .
.综上知,当m∈
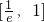 ∪(1,e],即0<lnm≤1或-1≤lnm<0时,g(x)的值域为闭区间.
∪(1,e],即0<lnm≤1或-1≤lnm<0时,g(x)的值域为闭区间.分析:(1)由于 函数f(x)=
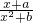 是定义在实数集R上的奇函数,则f(-x)=-f(x),构造方程,可求a与b值;
是定义在实数集R上的奇函数,则f(-x)=-f(x),构造方程,可求a与b值;(2)由题意以及①当x∈[0,3)时,g(x)=f(x);②g(x+3)=g(x)lnm(m≠1).得到
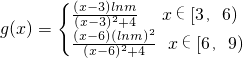 ;
;对参数lnm分类讨论,再依据函数g(x)在x∈[0,+∞)上的值域是闭区间,即可得到m的取值范围.
点评:本题考查的知识点是函数奇偶性,函数的值域,解题的关键是熟练掌握函数奇偶性的性质,以及分类讨论求出参数的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x+1)是偶函数,当x2>x1>1时,[f(x2)-f(x1)]( x2-x1)>0恒成立,设a=f (-
),b=f(2),c=f(3),则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |