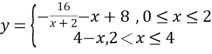题目内容
【题目】定义域为![]() 的函数
的函数![]() 满足
满足![]() ,当
,当![]() 时,
时,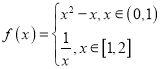 .若
.若![]() 时,
时,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由f(x+2)=2f(x)-1,求出x∈(2,3),以及x∈[3,4]的函数的解析式,分别求出(0,4]内的四段的最小值和最大值,注意运用二次函数的最值和函数的单调性,再由![]() 恒成立即为
恒成立即为![]() ,
,![]() ,解不等式即可得到所求范围
,解不等式即可得到所求范围
当x∈(2,3),则x2∈(0,1),
则f(x)=2f(x2)1=2(x2)22(x2)1,
即为f(x)=2x210x+11,
当x∈[3,4],则x2∈[1,2],
则f(x)=2f(x2)1=![]() .
.
当x∈(0,1)时,当x=![]() 时,f(x)取得最小值,且为
时,f(x)取得最小值,且为![]() ;
;
当x∈[1,2]时,当x=2时,f(x)取得最小值,且为![]() ;
;
当x∈(2,3)时,当x=![]() 时,f(x)取得最小值,且为
时,f(x)取得最小值,且为![]() ;
;
当x∈[3,4]时,当x=4时,f(x)取得最小值,且为0.
综上可得,f(x)在(0,4]的最小值为![]() .
.
若x∈(0,4]时, ![]() 恒成立,
恒成立,
则有![]() .
.
解得![]() .
.
当x∈(0,2)时,f(x)的最大值为1,
当x∈(2,3)时,f(x)∈[![]() ,1),
,1),
当x∈[3,4]时,f(x)∈[0,1],
即有在(0,4]上f(x)的最大值为1.
由![]() ,即为
,即为![]() ,解得
,解得![]() ,
,
综上,即有实数t的取值范围是![]() .
.
故选:C.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件 | 0 | 1 | 2 | 3 | 4 |
对应的天数/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生产的次品数/件 | 0 | 1 | 2 | 3 |
对应的天数/天 | 30 | 25 | 25 | 20 |
(1)将甲每天生产的次品数记为![]() (单位:件),日利润记为
(单位:件),日利润记为![]() (单位:元),写出
(单位:元),写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如果将统计的100天中产生次品量的频率作为概率,记![]() 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量
表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】我们把活跃网店数量较多的村庄称为淘宝村,随着电子商务在中国的发展,不少农村出现了一批专业的淘宝村,已知某乡镇有多个淘宝村,现从该乡镇淘宝村中随机抽取![]() 家商户,统计他们某一周的销售收入,结果统计如下:
家商户,统计他们某一周的销售收入,结果统计如下:
销售收入(收入) |
|
|
|
|
商户数 |
|
|
|
|
(1)从这![]() 家商户中按该周销售收入超过
家商户中按该周销售收入超过![]() 万元与不超过
万元与不超过![]() 万元分为
万元分为![]() 组,按分层抽样从中抽取
组,按分层抽样从中抽取![]() 家参加经验交流会,并从这
家参加经验交流会,并从这![]() 家中选
家中选![]() 家进行发言,求选出的
家进行发言,求选出的![]() 家恰有
家恰有![]() 家销售收入超过
家销售收入超过![]() 万元的概率;
万元的概率;
(2)若这![]() 家商户中有
家商户中有![]() 家商户入驻两家网购平台,其中
家商户入驻两家网购平台,其中![]() 家销售收入高于
家销售收入高于![]() 万元,完成下面的
万元,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“销售收入是否高于
的把握认为“销售收入是否高于![]() 万元与入驻两家网购平台有关”?
万元与入驻两家网购平台有关”?
入驻两家网购平台 | 仅入驻一家网购平台 | 合计 | |
销售收入高于 | |||
销售收入不高于 | |||
合计 |
附: .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|