题目内容
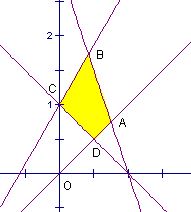 已知x,y满足:
已知x,y满足:
|
| xy |
| x2+y2 |
分析:由题意,借助已知动点在区域内任意动,而所求式子z=
=
,匿其中式子k=
的形式可以联想成在单位圆上动点P与原点构成的直线的斜率,进而求解.
| xy |
| y2-x2 |
| 1 | ||
k-
|
| y |
| x |
解答: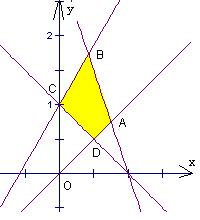 解z=
解z=
=
=
,其中k=
.
作出可行域得kOA<k<kOC,即k>1,
又因为函数u=k-
在(1,+∞)上单调增,所以u>0,所以z>0.
故答案为:0<z<+∞
 解z=
解z=| xy |
| y2-x2 |
| k |
| k 2-1 |
| 1 | ||
k-
|
| y |
| x |
作出可行域得kOA<k<kOC,即k>1,
又因为函数u=k-
| 1 |
| k |
故答案为:0<z<+∞
点评:此题重点考查了简单线性规划、已知两点坐标写斜率,及直线斜率的变化关系,还考查了利用几何思想解决代数式子的等价转化的思想.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知x,y满足
,则2x-y的取值范围是( )
|
| A、[-6,0] |
| B、[-6,-1] |
| C、[-5,-1] |
| D、[-5,0] |