Question

已知x，y满足

-4≤x-y≤-2 2≤x+y≤4

，则2x-y的取值范围是（　　）

• A、[-6，0]
• B、[-6，-1]
• C、[-5，-1]
• D、[-5，0]

Answer 1

分析：画出满足已知中约束条件的可行域，并求出各角点的坐标，代入目标函数后，比较目标函数值的大小后，可得答案．

解答：解：满足

-4≤x-y≤-2 2≤x+y≤4

的可行域，如下图所示：

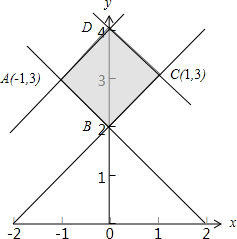
∵目标函数Z=2x-y
∴Z_A=-5，Z_B=-2，Z_C=-1，Z_D=-4，
故2x-y的最大值是-1，最小值是-5，
2x-y的取值范围是[-5，-1]
故选：C

点评：本题考查的知识点是简单线性规划，其中画出满足条件的可行域是解答的关键．