题目内容
已知f(x)是定义在实数集R上的增函数,且f(1)=0,函数g(x)在(-∞,1]上为增函数,在[1,+∞)上为减函数,且g(4)=g(0)=0,则集合{x|f(x)g(x)≥0}等于( )
| A.{x|x≤0或1≤x≤4} |
| B.{x|0≤x≤4} |
| C.{x|x≤4} |
| D.{x|0≤x≤1或x≥4} |
A
解析

练习册系列答案
相关题目
已知函数 ,
, ,若在区间
,若在区间 内,函数
内,函数 与
与 轴有3个不同的交点,则实数
轴有3个不同的交点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
下列函数中,既是奇函数又是增函数的为( )
| A.y=x+1 | B.y=-x3 |
C.y= | D.y=x|x| |
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
已知函数f(x)= 为奇函数,则f(g(-1))=( )
为奇函数,则f(g(-1))=( )
| A.-20 | B.-18 | C.-15 | D.17 |
 ,则
,则 的图象大致为( )
的图象大致为( )
 的棱长是1,点
的棱长是1,点 是对角线
是对角线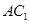 上一动点,记
上一动点,记 (
( ),过点
),过点 的截面将正方体分成两部分,其中点
的截面将正方体分成两部分,其中点 所在的部分的体积为
所在的部分的体积为 ,则函数
,则函数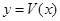 的图像大致为( )
的图像大致为( )




 对任意x∈R恒成立,则f(2011)等于( )
对任意x∈R恒成立,则f(2011)等于( )