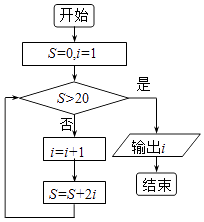
题目内容
【题目】已知函数f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a﹣1,2a],则( )
A.![]() ,b=0
,b=0
B.a=﹣1,b=0
C.a=1,b=1
D.a= ![]() ,b=﹣1
,b=﹣1
【答案】A
【解析】解:因为f(x)=ax2+bx+3a+b是偶函数,所以定义域关于原点对称,所以a﹣1+2a=0,解得a= ![]() .
.
所以f(x)= ![]() x2+bx+1+b,因为函数为偶函数,所以f(﹣x)=f(x),
x2+bx+1+b,因为函数为偶函数,所以f(﹣x)=f(x),
即) ![]() x2﹣bx+1+b=
x2﹣bx+1+b= ![]() x2+bx+1+b,所以2bx=0,解得b=0.
x2+bx+1+b,所以2bx=0,解得b=0.
所以答案是:A.
【考点精析】解答此题的关键在于理解函数的偶函数的相关知识,掌握一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.

练习册系列答案
相关题目