题目内容
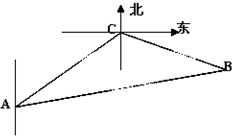
一缉私艇发现在北偏东45°方向,距离10nmile的海面上有一走私船正以10nmile/h的速度沿东偏南15°方向逃窜.缉私艇的速度为10
nmile/h,若在最短的时间t内追上该走私船,缉私艇应延北偏东45°+α的方向去追,求追及所需的时间t和α角.
| 3 |

设A,C分别表示缉私艇,走私船的位置,设经过 x小时后在B处追上,
则有AB=10
x,BC=10x,∠ACB=120°.
∴(10
x)2=102+(10x)2-200xcos120°,
∴x=1,
∴AB=10
,BC=10,
∴sinα=
=
,
∴α=30°.
则有AB=10
| 3 |
∴(10
| 3 |
∴x=1,
∴AB=10
| 3 |
∴sinα=
| BCsinα |
| AB |
| 1 |
| 2 |
∴α=30°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
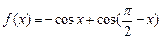 ,
,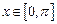 ,求函数
,求函数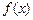 的最大值与最小值及此时x的值;
的最大值与最小值及此时x的值;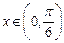 ,且
,且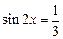 ,求
,求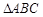 中,
中,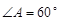 ,
,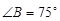 ,
,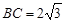 ,则
,则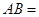 .
.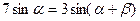 ,求证:
,求证: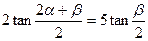 .
.