题目内容
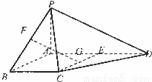
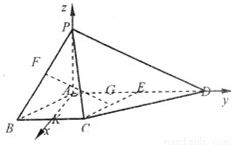
四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G,F分别是线段CE,PB上的动点,且满足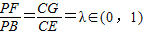 .
.(1)求证:PG∥平面PDC;
(2)求λ的值,使得二面角F-CD-G的余弦值为
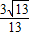 .
.
【答案】分析:(1)在平面PBC内过点F作直线FM∥PC,交BC于点M,连接MG,BE,则有 ,由
,由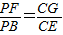 ,知GM∥BE,由E为AD的中点,ABCE为菱形,知BC∥DE,BC=DE,由此能够证明FG∥平面PDC.
,知GM∥BE,由E为AD的中点,ABCE为菱形,知BC∥DE,BC=DE,由此能够证明FG∥平面PDC.
(2)取BC的中点为K,以点A为原点,射线AK为x轴正半轴,AD为y轴正半轴,建立空间直角坐标系A-xyz,设PA=2,由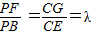 ,得
,得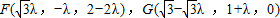 ,
,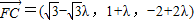 ,
,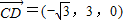 ,设平面FCD的法向量
,设平面FCD的法向量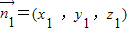 ,由
,由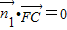 ,
,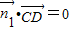 ,得
,得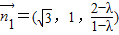 ,由平面GCD的法向量
,由平面GCD的法向量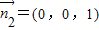 ,二面角F-CD-G的余弦值为
,二面角F-CD-G的余弦值为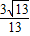 ,知|cos<
,知|cos<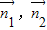 >|=|
>|=|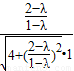 |=
|=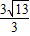 ,由此能求出λ.
,由此能求出λ.
解答:(1)证明:在平面PBC内过点F作直线FM∥PC,交BC于点M,
连接MG,BE,则有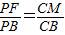 ,
,
∵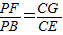 ,∴
,∴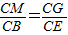 ,∴GM∥BE,
,∴GM∥BE,
∵E为AD的中点,ABCE为菱形,
∴BC∥DE,BC=DE,
∴CD∥BE∥GM,
∵FM∥PC,FM∩MG=M,且CD∩PC=C,
∴平面FGM∥平面PDC,
∵FG?平面FGM,∴FG∥平面PDC.

(2)解:取BC的中点为K,以点A为原点,射线AK为x轴正半轴,AD为y轴正半轴,
建立如图所示的空间直角坐标系A-xyz,设PA=2,则A(0,0,0),P(0,0,2),D(0,4,0),
由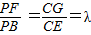 ,得
,得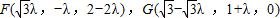 ,
,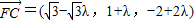 ,
,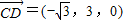 ,
,
设平面FCD的法向量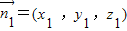 ,则
,则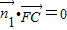 ,
,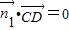 ,
,
即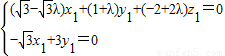 ,
,
∴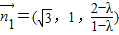 ,
,
∵平面GCD的法向量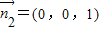 ,二面角F-CD-G的余弦值为
,二面角F-CD-G的余弦值为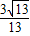 ,
,
∴|cos<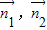 >|=|
>|=|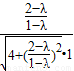 |=
|=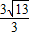 ,
,
整理,得8λ2-14λ+5=0,
解得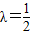 ,或
,或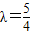 ,
,
∵0<λ<1,∴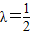 .
.
点评:本题考查直线与平面平行的证明,求实数的值,使得二面角的余弦值为定值.解题时要认真审题,仔细解答,注意向量法的合理运用.
 ,由
,由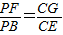 ,知GM∥BE,由E为AD的中点,ABCE为菱形,知BC∥DE,BC=DE,由此能够证明FG∥平面PDC.
,知GM∥BE,由E为AD的中点,ABCE为菱形,知BC∥DE,BC=DE,由此能够证明FG∥平面PDC.(2)取BC的中点为K,以点A为原点,射线AK为x轴正半轴,AD为y轴正半轴,建立空间直角坐标系A-xyz,设PA=2,由
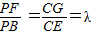 ,得
,得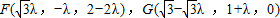 ,
,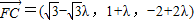 ,
,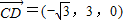 ,设平面FCD的法向量
,设平面FCD的法向量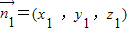 ,由
,由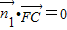 ,
,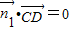 ,得
,得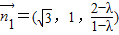 ,由平面GCD的法向量
,由平面GCD的法向量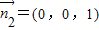 ,二面角F-CD-G的余弦值为
,二面角F-CD-G的余弦值为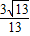 ,知|cos<
,知|cos<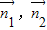 >|=|
>|=|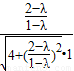 |=
|=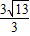 ,由此能求出λ.
,由此能求出λ.解答:(1)证明:在平面PBC内过点F作直线FM∥PC,交BC于点M,
连接MG,BE,则有
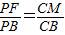 ,
,∵
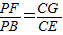 ,∴
,∴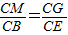 ,∴GM∥BE,
,∴GM∥BE,∵E为AD的中点,ABCE为菱形,
∴BC∥DE,BC=DE,
∴CD∥BE∥GM,
∵FM∥PC,FM∩MG=M,且CD∩PC=C,
∴平面FGM∥平面PDC,
∵FG?平面FGM,∴FG∥平面PDC.

(2)解:取BC的中点为K,以点A为原点,射线AK为x轴正半轴,AD为y轴正半轴,
建立如图所示的空间直角坐标系A-xyz,设PA=2,则A(0,0,0),P(0,0,2),D(0,4,0),
由
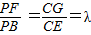 ,得
,得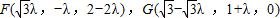 ,
,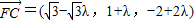 ,
,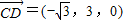 ,
,设平面FCD的法向量
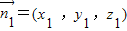 ,则
,则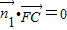 ,
,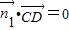 ,
,即
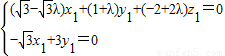 ,
,∴
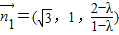 ,
,∵平面GCD的法向量
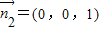 ,二面角F-CD-G的余弦值为
,二面角F-CD-G的余弦值为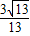 ,
,∴|cos<
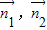 >|=|
>|=|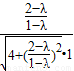 |=
|=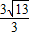 ,
,整理,得8λ2-14λ+5=0,
解得
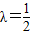 ,或
,或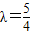 ,
,∵0<λ<1,∴
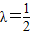 .
.
点评:本题考查直线与平面平行的证明,求实数的值,使得二面角的余弦值为定值.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
相关题目
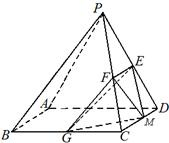 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.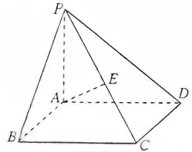 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2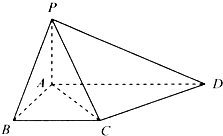 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.