题目内容
已知直线ax﹣by﹣2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则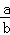 为( )
为( )
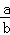 为( )
为( )| A.3 | B.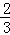 | C.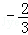 | D.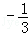 |
D
试题分析:由导数的几何意义可求曲线y=x3在(1,1)处的切线斜率k,然后根据直线垂直的条件可求
 的值. 解:设曲线y=x3在点P(1,1)处的切线斜率为k,则k=f′(1)=3
的值. 解:设曲线y=x3在点P(1,1)处的切线斜率为k,则k=f′(1)=3因为直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,
 ,故选D.
,故选D.点评:本题主要考查了导数的几何意义:曲线在点(x0,y0)处的切线斜率即为该点处的导数值,两直线垂直的条件的运用.属于基础试题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
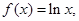 若存在函数
若存在函数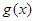 使得
使得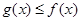 恒成立,则称
恒成立,则称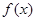 的一个“下界函数”.
的一个“下界函数”.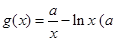 为实数
为实数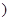 为
为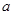 的取值范围;
的取值范围;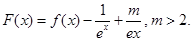 试问函数
试问函数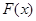 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由. ,有下列说法:
,有下列说法: 上一点
上一点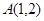 ,则点
,则点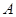 处的切线斜率等于
处的切线斜率等于
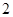
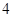
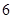
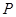 在曲线
在曲线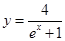 上,
上,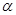 为曲线在点
为曲线在点



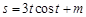 (
(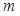 为常数),则其速度方程为( )
为常数),则其速度方程为( )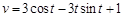
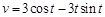
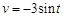
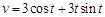
 等于
等于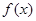 与
与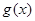 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若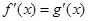 ,则
,则
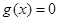
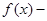
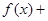
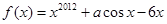 ,且
,且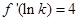 ,则
,则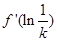 =( )
=( )