题目内容
已知a＞0,设命题p：函数y=ax在R上单调递减，q：不等式x+|x-2a|＞1的解集为R，若p和q中有且只有一个命题为真命题，求a的取值范围.
a的取值范围是0＜a≤
或a≥1
或a≥1由函数y=ax在R上单调递减知0＜a＜1，所以命题p为真命题时a的取值范围是0＜a＜1，令y=x+|x-2a|，
则y=
不等式x+|x-2a|＞1的解集为R，只要ymin＞1即可，而函y在R上的最小值为2a,所以2a＞1，即a＞.即q真
a＞.
所以命题p和q有且只有一个命题正确时a的取值范围是0＜a≤或a≥1.
则y=
不等式x+|x-2a|＞1的解集为R，只要ymin＞1即可，而函y在R上的最小值为2a,所以2a＞1，即a＞.即q真a＞.所以命题p和q有且只有一个命题正确时a的取值范围是0＜a≤
或a≥1.
练习册系列答案
相关题目
B”；
p”命题，并判断它们的真假。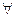
x，x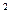
＋4x＋4≥0； （2）p：
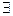x，x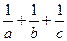
=2求证：a、b、c中至少有两上不小于1.
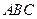不是等腰三角形，则它的任何两个内角不相等”的逆否命题 是 ；
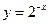与函数
的图像关于直线
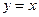对称．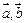
共线，则向量
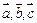两两共面，则向量