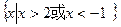题目内容
用反证法证明:
设三个正实数a、b、c满足条件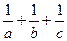 =2求证:a、b、c中至少有两上不小于1.
=2求证:a、b、c中至少有两上不小于1.
设三个正实数a、b、c满足条件
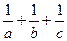 =2求证:a、b、c中至少有两上不小于1.
=2求证:a、b、c中至少有两上不小于1.证明略
[解题思路]:用反证法证题时作出正确的反设是前提,“a, b, c中至多有一个数不小于1”的反设为“a, b, c中至多有一个数不小于1”,有两种情况“a、b、c三数均小于1”和“a、b、c中有两数小于1”;而推出矛盾是关键,也是难点.
假设a, b, c中至多有一个数不小于1,这包含下面两种情况:
(1)a、b、c三数均小于1,
即0<a<1 , 0<b<1, 0<c<1,则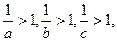
∴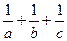 >3与已知条件矛盾;
>3与已知条件矛盾;
(2)a、b、c中有两数小于1,
设0<a<1, 0<b<1,而c≥1,则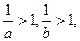
∴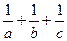 >2+
>2+ >2,也与已知条件矛盾;
>2,也与已知条件矛盾;
∴假设不成立,∴a、b、c中至少有两个不小于1.
【名师指引】利用互为逆否的两个命题同真同假的关系,将不易判断真假的命题,转化为判断其逆否命题的真假(尤其是对否定式语句的命题),充分利用等价转化的思想方法。正确的反设是(即否定结论)是正确运用反证法的前提,要注意一些常用的“结论否定形式”,另外,需注意作出的反设必须包括与结论相反的所有情况。
假设a, b, c中至多有一个数不小于1,这包含下面两种情况:
(1)a、b、c三数均小于1,
即0<a<1 , 0<b<1, 0<c<1,则
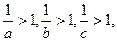
∴
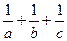 >3与已知条件矛盾;
>3与已知条件矛盾;(2)a、b、c中有两数小于1,
设0<a<1, 0<b<1,而c≥1,则
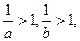
∴
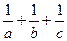 >2+
>2+ >2,也与已知条件矛盾;
>2,也与已知条件矛盾;∴假设不成立,∴a、b、c中至少有两个不小于1.
【名师指引】利用互为逆否的两个命题同真同假的关系,将不易判断真假的命题,转化为判断其逆否命题的真假(尤其是对否定式语句的命题),充分利用等价转化的思想方法。正确的反设是(即否定结论)是正确运用反证法的前提,要注意一些常用的“结论否定形式”,另外,需注意作出的反设必须包括与结论相反的所有情况。

练习册系列答案
相关题目
 ,设P:函数
,设P:函数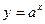 在R上递增,Q:复数Z=(
在R上递增,Q:复数Z=(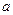 -4) +
-4) + 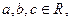 则“
则“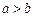 ”是“
”是“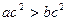 ”成立的充分不必要条件;
”成立的充分不必要条件;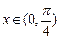 时,函数
时,函数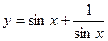 的最小值为2;
的最小值为2;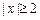 ,则
,则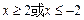 ”的否命题是“若
”的否命题是“若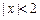 ,则
,则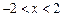 ”;
”;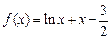 在区间(1,2)上有且仅有一个零点。
在区间(1,2)上有且仅有一个零点。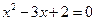 ,则
,则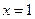 或
或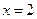 ;②若
;②若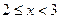 ,则
,则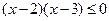 ;
;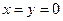 ,则
,则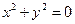 ;
;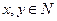 ,且
,且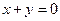 是奇数,则
是奇数,则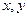 中一个是奇数,一个是偶数,那么( ).
中一个是奇数,一个是偶数,那么( ).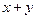 为有理数,则
为有理数,则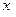 、
、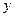 也都是有理数”;
也都是有理数”;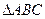 ∽
∽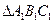 ”.
”.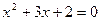 的根是
的根是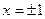 ;
;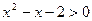 的解集是
的解集是