题目内容
关于函数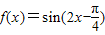 ,有下列命题:
,有下列命题:①其表达式可写成
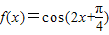 ;
;②直线
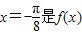 图象的一条对称轴;
图象的一条对称轴;③f(x)的图象可由g(x)=sin2x的图象向右平移
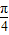 个单位得到;
个单位得到;④存在α∈(0,π),使f(x+α)=f(x+3α)恒成立
则其中真命题为( )
A.②③
B.①②
C.②④
D.③④
【答案】分析:①将两函数解析式化简整理,若表示同一个函数,则①正确,否则错误.
②若 时,f(x)取得最值,则②正确.否则错误.
时,f(x)取得最值,则②正确.否则错误.
③根据左加右减原则,写出平移后图象对应的解析式,进行对照可以断定正误
④考虑先取特殊值,比如取α= 等进行验证.
等进行验证.
解答:解: =
=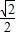 (sin2x-cos2x).
(sin2x-cos2x).
 =
= (cos2x-sin2x).与原函数不为同一个函数,①错误.
(cos2x-sin2x).与原函数不为同一个函数,①错误.
② 时,f(x)=sin[2×(
时,f(x)=sin[2×(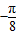 )-
)- ]=sin(-
]=sin(-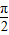 )=-1,函数取得最小值,所以直线
)=-1,函数取得最小值,所以直线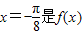 图象的一条对称轴.②正确
图象的一条对称轴.②正确
③将g(x)=sin2x的图象向右平移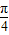 个单位得到,得到图象对应的解析式是y=sin2(x-
个单位得到,得到图象对应的解析式是y=sin2(x- )=sin(2x-
)=sin(2x-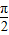 )=-cos2x,与f(x)不为同一个函数.③错误.
)=-cos2x,与f(x)不为同一个函数.③错误.
④取α=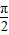 ,f(x+α)=f(x+
,f(x+α)=f(x+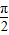 )=
)= =sin(2x+
=sin(2x+ ),f(x+3α)=f(x+3•
),f(x+3α)=f(x+3• )=
)= =sin(2x+3π-
=sin(2x+3π- )=sin(2x+2π+π-
)=sin(2x+2π+π- )=sin(2x+
)=sin(2x+ ),
),
所以存在取α= ∈(0,π),使f(x+α)=f(x+3α)恒成立. ④正确.
∈(0,π),使f(x+α)=f(x+3α)恒成立. ④正确.
故选C.
点评:本题考查三角函数图象性质,三角函数式的化简,三角函数图象变换.在图象平移变换中,针对的是x的变化,③中,平移后相位应由2x变化为2(x- )即为2x-
)即为2x- ,而不是2x-
,而不是2x- .
.
②若
 时,f(x)取得最值,则②正确.否则错误.
时,f(x)取得最值,则②正确.否则错误.③根据左加右减原则,写出平移后图象对应的解析式,进行对照可以断定正误
④考虑先取特殊值,比如取α=
 等进行验证.
等进行验证.解答:解:
 =
=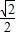 (sin2x-cos2x).
(sin2x-cos2x). =
= (cos2x-sin2x).与原函数不为同一个函数,①错误.
(cos2x-sin2x).与原函数不为同一个函数,①错误.②
 时,f(x)=sin[2×(
时,f(x)=sin[2×(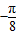 )-
)- ]=sin(-
]=sin(-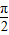 )=-1,函数取得最小值,所以直线
)=-1,函数取得最小值,所以直线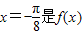 图象的一条对称轴.②正确
图象的一条对称轴.②正确③将g(x)=sin2x的图象向右平移
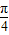 个单位得到,得到图象对应的解析式是y=sin2(x-
个单位得到,得到图象对应的解析式是y=sin2(x- )=sin(2x-
)=sin(2x-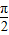 )=-cos2x,与f(x)不为同一个函数.③错误.
)=-cos2x,与f(x)不为同一个函数.③错误.④取α=
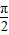 ,f(x+α)=f(x+
,f(x+α)=f(x+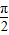 )=
)= =sin(2x+
=sin(2x+ ),f(x+3α)=f(x+3•
),f(x+3α)=f(x+3• )=
)= =sin(2x+3π-
=sin(2x+3π- )=sin(2x+2π+π-
)=sin(2x+2π+π- )=sin(2x+
)=sin(2x+ ),
),所以存在取α=
 ∈(0,π),使f(x+α)=f(x+3α)恒成立. ④正确.
∈(0,π),使f(x+α)=f(x+3α)恒成立. ④正确.故选C.
点评:本题考查三角函数图象性质,三角函数式的化简,三角函数图象变换.在图象平移变换中,针对的是x的变化,③中,平移后相位应由2x变化为2(x-
 )即为2x-
)即为2x- ,而不是2x-
,而不是2x- .
. 
练习册系列答案
相关题目
 ,有下列命题:①f(x)的最大值为
,有下列命题:①f(x)的最大值为 ;②f(x)是以π为最小正周期的周期函数;③f(x)在区间(
;②f(x)是以π为最小正周期的周期函数;③f(x)在区间( ,
, )上单调递减;④将函数y=
)上单调递减;④将函数y= cos2x的图象向左平移
cos2x的图象向左平移 个单位后,将与f(x)的图象重合,其中正确命题的序号是 .
个单位后,将与f(x)的图象重合,其中正确命题的序号是 . ,有下列命题
,有下列命题 ;
;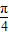 个单位而得到;
个单位而得到; ;
; 为单调递增函数;
为单调递增函数; ,有下列命题:
,有下列命题: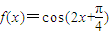 ;
; 图象的一条对称轴;
图象的一条对称轴;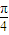 个单位得到;
个单位得到; ,有下列命题:
,有下列命题: 轴对称;
②当
轴对称;
②当 时,
时, 是增函数;当
是增函数;当 时,
时, ; ④当
; ④当 和
和 时,
时, ,有下列命题:
,有下列命题: 的表达式可以变换成
的表达式可以变换成
 ;
;
 为最小正周期的周期函数;
为最小正周期的周期函数; 对称;
④
对称;
④ 对称.
对称.