题目内容
关于函数 ,有下列命题
,有下列命题①其最小正周期为
 ;
;②其图象由y=2sin3x向右平移
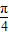 个单位而得到;
个单位而得到;③其表达式写成
 ;
;④在
 为单调递增函数;
为单调递增函数;则其中真命题为 .
【答案】分析:①根据周期公式和解析式求出,②由图象变换法则“左加右减”求出平移后的解析式,③利用诱导公式实现正弦函数和余弦函数的转化,④由函数的定义域求出整体“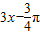 ”的范围,再由正弦函数的单调性进行判断.
”的范围,再由正弦函数的单调性进行判断.
解答:解:①由ω=3知函数的周期是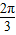 ,故①正确;
,故①正确;
②由y=2sin3x的图象向右平移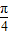 ,得到函数y=2sin3(x-
,得到函数y=2sin3(x-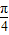 )=
)=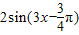 的图象,故②正确;
的图象,故②正确;
③因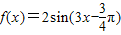 =
=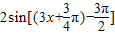 =
=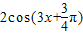 ,故③正确;
,故③正确;
④由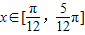 得,
得,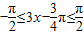 ,故函数在
,故函数在 上递增,故④正确.
上递增,故④正确.
故答案为:①②③④.
点评:本题考查了复合三角函数的性质问题,即函数的周期性、函数图象变换、诱导公式的利用和整体思想,主要利用正弦(余弦)函数的性质来判断.
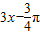 ”的范围,再由正弦函数的单调性进行判断.
”的范围,再由正弦函数的单调性进行判断.解答:解:①由ω=3知函数的周期是
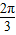 ,故①正确;
,故①正确;②由y=2sin3x的图象向右平移
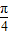 ,得到函数y=2sin3(x-
,得到函数y=2sin3(x-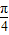 )=
)=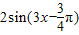 的图象,故②正确;
的图象,故②正确;③因
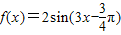 =
=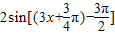 =
=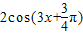 ,故③正确;
,故③正确;④由
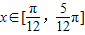 得,
得,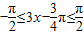 ,故函数在
,故函数在 上递增,故④正确.
上递增,故④正确.故答案为:①②③④.
点评:本题考查了复合三角函数的性质问题,即函数的周期性、函数图象变换、诱导公式的利用和整体思想,主要利用正弦(余弦)函数的性质来判断.

练习册系列答案
相关题目
 ,有下列命题:①f(x)的最大值为
,有下列命题:①f(x)的最大值为 ;②f(x)是以π为最小正周期的周期函数;③f(x)在区间(
;②f(x)是以π为最小正周期的周期函数;③f(x)在区间( ,
, )上单调递减;④将函数y=
)上单调递减;④将函数y= cos2x的图象向左平移
cos2x的图象向左平移 个单位后,将与f(x)的图象重合,其中正确命题的序号是 .
个单位后,将与f(x)的图象重合,其中正确命题的序号是 . ,有下列命题:
,有下列命题: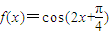 ;
; 图象的一条对称轴;
图象的一条对称轴;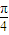 个单位得到;
个单位得到; ,有下列命题:
,有下列命题: 轴对称;
②当
轴对称;
②当 时,
时, 是增函数;当
是增函数;当 时,
时, ; ④当
; ④当 和
和 时,
时, ,有下列命题:
,有下列命题: 的表达式可以变换成
的表达式可以变换成
 ;
;
 为最小正周期的周期函数;
为最小正周期的周期函数; 对称;
④
对称;
④ 对称.
对称.