题目内容
已知以原点D为中心,F( ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,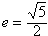 。
。
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,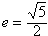 。
。
(1)求双曲线C的标准方程及其渐近线方程;
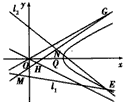
(2)如图,已知过点M(x1,y1)的直线l1:x1x+4y1y=4与过点N(x2,y2)(其中x2≠x1)的直线l2:x2x+4y2y=4的交点E在双曲线C上,直线MN与两条渐近 线分别交于G、H两点,求△OGH的面积。
(2)如图,已知过点M(x1,y1)的直线l1:x1x+4y1y=4与过点N(x2,y2)(其中x2≠x1)的直线l2:x2x+4y2y=4的交点E在双曲线C上,直线MN与两条渐近 线分别交于G、H两点,求△OGH的面积。
解:(1)设C的标准方程为 则由题意 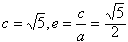 因此 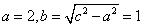 C的标准方程为 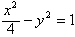 C的渐近线方程为 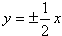 ,即x-2y=0和x+2y=0; ,即x-2y=0和x+2y=0; |
|
| (2)如图,由题意点E(xE,yE)在直线l1:x1x+4y1y=4和l2:x2x+4y2y=4上,因此有x1xE+4y1yE=4,x2xE+4y2yE=4 故点M、N均在直线xEx+4yEy=4上,因此直线MN的方程为xEx+4yEy=4 设G、H分别是直线MN与渐近线x-2y=0及x+2y=0的交点,由方程组  及 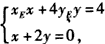 解得: 解得: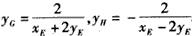 设MN与x轴的交点为Q,则在直线xEx+4yEy=4中,令y=0 得 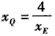 (易知xE≠0),注意到xE2-4yE2=4,得  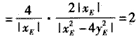 。 。 |
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知以原点O为中心的椭圆的一条准线方程为
已知以原点O为中心的椭圆的一条准线方程为 ,离心率
,离心率 ,M是椭圆上的动点,
,M是椭圆上的动点, ),(0,
),(0, ),求|MC|·|MD|的最大值;
),求|MC|·|MD|的最大值; ,
, ,求线段QB的中点P的轨迹方程。
,求线段QB的中点P的轨迹方程。 
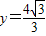 ,离心率
,离心率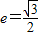 ,M是椭圆上的动点
,M是椭圆上的动点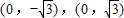 ,求|MC|•|MD|的最大值;
,求|MC|•|MD|的最大值;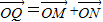 ,
,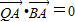 、求线段QB的中点P的轨迹方程.
、求线段QB的中点P的轨迹方程.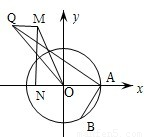
 ,离心率
,离心率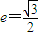 ,M是椭圆上的动点
,M是椭圆上的动点 ,求|MC|•|MD|的最大值;
,求|MC|•|MD|的最大值;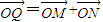 ,
, 、求线段QB的中点P的轨迹方程.
、求线段QB的中点P的轨迹方程.