题目内容
已知函数f(x)=px2+qx,其中p>0,p+q>1,对于数列{an},设它的前n项和为Sn,且满足Sn=f(n)(n∈N*).(1)求数列{an}的通项公式,并证明an+1>an>1(n∈N*);
(2)求证:点
 在同一直线l1上;
在同一直线l1上;(3)若过点N1(1,a1),N2(2,a2)作直线l2,设l2与l1的夹角为θ,求tanθ的最大值.
【答案】分析:(1)由“当n=1时,a1=s1;当n≥2时,an=Sn-Sn-1”,求出通项公式an,再由p>0,p+q>1进行证明;
(2)根据一条直线的斜率是一个定值,即在所给的点中任选两点求出是定值进行证明;
(3)由斜率公式求出直线l2的斜率,再由(2)和夹角公式表示夹角的正切,化简后利用基本不等式求出最大值,注意等号成立的条件.
解答:解:(1)∵Sn=f(n)=pn2+qn∴当n=1时,a1=s1=p+q
当n≥2时,an=Sn-Sn-1=pn2+qn-[p(n-1)2+q(n-1)]=2pn-p+q
由于n=1时,a1=p+q适合上式,故数列{an}的通项公式为an=2pn-p+q…(3分)
又∵an+1-an=2p>0,
∴{an}是首项为p+q,公差为2p的等差数列,∴an+1>an>…>a1=p+q>1,
∴an+1>an>1…(4分)
(2)设Mi,Mj(i≠j)是M1,M2,…,Mn中任意两点,则
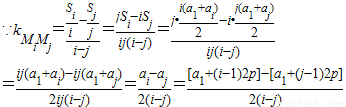
=P…(8分)
∴Mi,Mj两点连线的斜率为定值P,又Mi,Mj是M1,M2,…,Mn中任意两点,
∴点M1,M2,…,Mn在同一直线l1上…(9分)
(3)∵N1,N2 两点连线的斜率为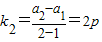 ,
,
又∵直线l1的斜率为k1=p,由夹角公式得
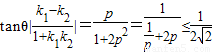 …(13分)
…(13分)
当且仅当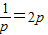 即
即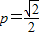 时,上式等号成立.
时,上式等号成立.
故当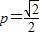 时,tanθ有最大值
时,tanθ有最大值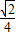 …(14分)
…(14分)
点评:本题是一道综合题,涉及了数列通项公式和前n项和公式之间的关系式,直线的斜率公式,两条相交直线的夹角公式,以及基本不等式求最值问题,综合性强,考查了分析问题、解决问题和知识的综合应用能力.
(2)根据一条直线的斜率是一个定值,即在所给的点中任选两点求出是定值进行证明;
(3)由斜率公式求出直线l2的斜率,再由(2)和夹角公式表示夹角的正切,化简后利用基本不等式求出最大值,注意等号成立的条件.
解答:解:(1)∵Sn=f(n)=pn2+qn∴当n=1时,a1=s1=p+q
当n≥2时,an=Sn-Sn-1=pn2+qn-[p(n-1)2+q(n-1)]=2pn-p+q
由于n=1时,a1=p+q适合上式,故数列{an}的通项公式为an=2pn-p+q…(3分)
又∵an+1-an=2p>0,
∴{an}是首项为p+q,公差为2p的等差数列,∴an+1>an>…>a1=p+q>1,
∴an+1>an>1…(4分)
(2)设Mi,Mj(i≠j)是M1,M2,…,Mn中任意两点,则

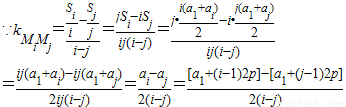
=P…(8分)
∴Mi,Mj两点连线的斜率为定值P,又Mi,Mj是M1,M2,…,Mn中任意两点,
∴点M1,M2,…,Mn在同一直线l1上…(9分)
(3)∵N1,N2 两点连线的斜率为
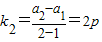 ,
,又∵直线l1的斜率为k1=p,由夹角公式得
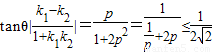 …(13分)
…(13分)当且仅当
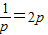 即
即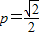 时,上式等号成立.
时,上式等号成立.故当
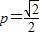 时,tanθ有最大值
时,tanθ有最大值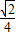 …(14分)
…(14分)点评:本题是一道综合题,涉及了数列通项公式和前n项和公式之间的关系式,直线的斜率公式,两条相交直线的夹角公式,以及基本不等式求最值问题,综合性强,考查了分析问题、解决问题和知识的综合应用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目