题目内容
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点.
的中点.
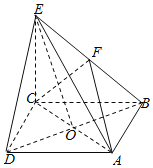
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接![]() ,利用中位线的性质得出
,利用中位线的性质得出![]() ,然后利用直线与平面平行的判定定理可证明出
,然后利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)由正方形的基本性质得出![]() ,由
,由![]() 平面
平面![]() 得出
得出![]() ,利用直线与平面垂直的判定定理证明出
,利用直线与平面垂直的判定定理证明出![]() 平面
平面![]() ,由此可得出
,由此可得出![]() ;
;
(3)取![]() 的中点
的中点![]() ,利用中位线的性质结合
,利用中位线的性质结合![]() 平面
平面![]() 得出
得出![]() 平面
平面![]() ,计算出
,计算出![]() 和
和![]() 的面积,然后利用锥体的体积公式可计算出三棱锥
的面积,然后利用锥体的体积公式可计算出三棱锥![]() 的体积.
的体积.
(1)连接![]() ,如下图:
,如下图:
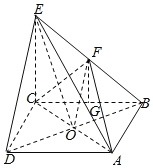
由四边形![]() 是正方形可知,点
是正方形可知,点![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)由![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是正方形可知,
是正方形可知,![]() .
.
又![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() ;
;
(3)取![]() 中
中![]() ,连接
,连接![]() ,在四棱锥
,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,
![]() 是
是![]() 的中位线,
的中位线,![]() ,
,![]() 底面
底面![]() .
.
![]() ,
,![]() .
.
因此,三棱锥![]() 的体积
的体积![]() .
.

【题目】某超市计划按月订购一种饮料,每天进货量相同,进货成本每瓶3元,售价每瓶5元,每天未售出的饮料最后打4折当天全部处理完![]() 根据往年销售经验,每天需求量与当天最高气温
根据往年销售经验,每天需求量与当天最高气温![]() 单位:
单位:![]() 有关
有关![]() 如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为100瓶
,需求量为300瓶;如果最高气温低于20,需求量为100瓶![]() 为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
![]() Ⅰ
Ⅰ![]() 求六月份这种饮料一天的需求量
求六月份这种饮料一天的需求量![]() 单位:瓶
单位:瓶![]() 的分布列,并求出期望EX;
的分布列,并求出期望EX;
![]() Ⅱ
Ⅱ![]() 设六月份一天销售这种饮料的利润为
设六月份一天销售这种饮料的利润为![]() 单位:元
单位:元![]() ,且六月份这种饮料一天的进货量为
,且六月份这种饮料一天的进货量为![]() 单位:瓶
单位:瓶![]() ,请判断Y的数学期望是否在
,请判断Y的数学期望是否在![]() 时取得最大值?
时取得最大值?
【题目】某家庭为了解冬季用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出用电量![]() 关于气温
关于气温![]() 的线性回归方程;
的线性回归方程;
(2)在这5天中随机抽取两天,求至少有一天用电量低于10(度)的概率.
(附:回归直线方程的斜率和截距的最小二乘法估计公式为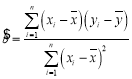 ,
,![]() )
)
