题目内容
10.已知函数f(x)=2sin($\frac{1}{3}$x+$\frac{π}{6}$)(x∈R).(1)求函数f(x)周期、单调性、对称点、对称轴.
(2)设0<α<$\frac{π}{2}$<β<π,f(3a+π)=$\frac{10}{13}$,f(3β+$\frac{5π}{2}$)=-$\frac{6}{5}$,求sin(α-β)的值.
分析 (1)根据三角函数单调性,对称中心和对称轴,周期的计算公式即可得到结论.
(2)根据条件求出sinα,cosα,sinβ,cosβ,利用两角和差的正弦公式进行求解即可.
解答 解:(1)函数的周期T=$\frac{2π}{\frac{1}{3}}$=6π,
由-$\frac{π}{2}$+2kπ≤$\frac{1}{3}$x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,
解得6kπ-2π≤x≤6kπ+π,即函数的递增区间为[6kπ-2π,6kπ+π],k∈Z,
由$\frac{π}{2}$+2kπ≤$\frac{1}{3}$x+$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,
解得6kπ+π≤x≤6kπ+$\frac{4π}{3}$,即函数的递减区间为[6kπ+π,6kπ++$\frac{4π}{3}$],k∈Z,
由2x+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,即x=$\frac{π}{12}$+kπ,k∈Z,
即函数的对称轴为x=$\frac{π}{12}$+kπ,k∈Z,
由2x+$\frac{π}{3}$=kπ,即x=-$\frac{π}{6}$+$\frac{kπ}{2}$,即函数的对称中心为(-$\frac{π}{6}$+$\frac{kπ}{2}$,0)
由$\frac{1}{3}$x+$\frac{π}{6}$=kπ得x=3kπ-$\frac{π}{2}$,即对称点为(3kπ-$\frac{π}{2}$,0),k∈Z,
由$\frac{1}{3}$x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,得x=3kπ+π,即对称轴为x=3kπ+π,k∈Z.
(2)∵f(3a+π)=2sin(α+$\frac{π}{2}$)=2cosα=$\frac{10}{13}$,
∴cosα=$\frac{5}{13}$,
∵f(3β+$\frac{5π}{2}$)=2sin(β+π)=-2sinβ=-$\frac{6}{5}$,
∴sinβ=$\frac{3}{5}$,
而0<α<$\frac{π}{2}$<β<π,
∴sinα=$\frac{12}{13}$,cosβ=-$\frac{4}{5}$,
∴sin(α-β)=sinαcosβ-cosαsinβ=$\frac{12}{13}$×(-$\frac{4}{5}$)-$\frac{5}{13}$×$\frac{3}{5}$=-$\frac{63}{65}$.
点评 本题主要考查三角函数求值以及三角函数的图象和性质,利用两角和差的正弦公式是解决本题的关键.

| A. | [0,1)∪(1,+∞) | B. | (-∞,1) | C. | (-∞,1)∪(1,+∞) | D. | (1,+∞) |
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
| A. | 3件都是正品 | B. | 至少有1次品 | C. | 3件都是次品 | D. | 至少有1件正品 |
 如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始向右移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.
如图,在△AOB中,点A(2,1),B(3,0),点E在射线OB上自O开始向右移动.设OE=x,过E作OB的垂线l,记△AOB在直线l左边部分的面积为S,试写出S与x的函数关系式,并画出大致的图象.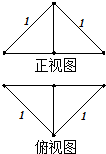 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.