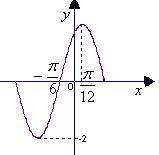
题目内容
已知
(Ⅰ)当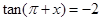 时,求
时,求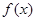 的值;
的值;
(Ⅱ)指出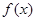 的最大值与最小值,并分别写出使
的最大值与最小值,并分别写出使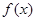 取得最大值、最小值的自变量
取得最大值、最小值的自变量 的集合.
的集合.

(Ⅰ)当
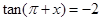 时,求
时,求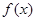 的值;
的值;(Ⅱ)指出
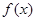 的最大值与最小值,并分别写出使
的最大值与最小值,并分别写出使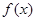 取得最大值、最小值的自变量
取得最大值、最小值的自变量 的集合.
的集合.(1)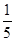 ;(2)最大值1,
;(2)最大值1,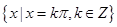 ;最小值0,
;最小值0, .
.
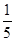 ;(2)最大值1,
;(2)最大值1,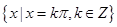 ;最小值0,
;最小值0, .
.本试题主要考查了三角函数中诱导公式的、同角三角关系式的运用,以及正余弦函数的最值的求解和运算的综合试题。诱导公式符合奇变偶不变符号看象限的原则,是化简的关键步骤。
解: (Ⅰ)
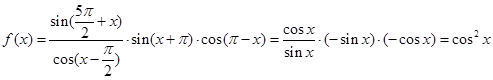
……………………3分
由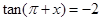 ,得
,得 . ……………………4分
. ……………………4分
所以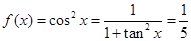 . ……………………6分
. ……………………6分
(Ⅱ)因为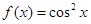 ,所以
,所以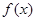 的最大值为1,最小值为0. …………8分
的最大值为1,最小值为0. …………8分
当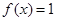 时,
时,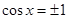 ,此时
,此时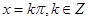 .
.
所以使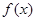 取得最大值的自变量
取得最大值的自变量 的集合为
的集合为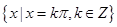 .
.
……………………10分
当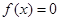 时,
时,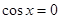 ,此时
,此时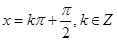 .
.
所以使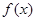 取得最小值的自变量
取得最小值的自变量 的集合为
的集合为 .………12分
.………12分
解: (Ⅰ)
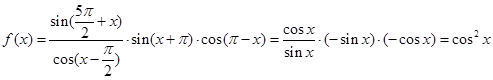
……………………3分
由
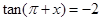 ,得
,得 . ……………………4分
. ……………………4分所以
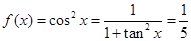 . ……………………6分
. ……………………6分(Ⅱ)因为
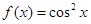 ,所以
,所以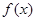 的最大值为1,最小值为0. …………8分
的最大值为1,最小值为0. …………8分当
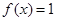 时,
时,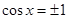 ,此时
,此时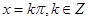 .
.所以使
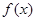 取得最大值的自变量
取得最大值的自变量 的集合为
的集合为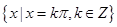 .
. ……………………10分
当
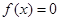 时,
时,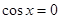 ,此时
,此时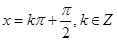 .
.所以使
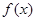 取得最小值的自变量
取得最小值的自变量 的集合为
的集合为 .………12分
.………12分
练习册系列答案
相关题目
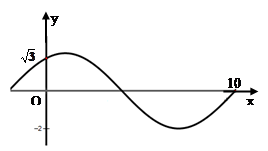
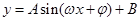 的一部分图像如图所示,如果
的一部分图像如图所示,如果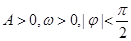 .
.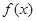 的解析式;
的解析式;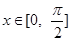 ,求
,求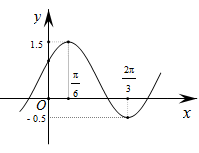
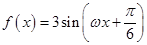 ,
,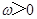 ,
,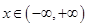 ,且以
,且以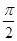 为最小正周期.
为最小正周期.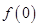 ;
; 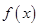 的解析式;
的解析式;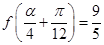 ,
,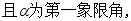 求
求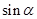 的值.
的值. ,其中
,其中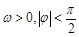 ,若
,若 ,且图象的一条对称轴离一个对称中心的最近距离是
,且图象的一条对称轴离一个对称中心的最近距离是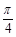 .
.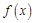 的解析式;
的解析式; 是
是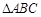 的三个内角,且
的三个内角,且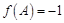 ,求
,求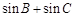 的取值范围
的取值范围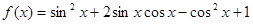
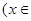 R
R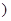 .
.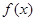 的最大值,并指出此时
的最大值,并指出此时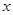 的值.
的值. 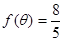 ,求
,求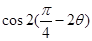 的值.
的值. )sin2x-2sin(x+
)sin2x-2sin(x+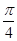 )sin(x-
)sin(x- ,
,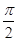 ],求f(x)的取值范围
],求f(x)的取值范围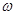 x+
x+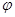 )(
)(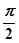
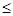
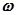 =( )
=( )



 为锐角,且cos
为锐角,且cos
 ,cos
,cos
 ,则
,则 的值是_____________.
的值是_____________.