Question

【题目】已知函数f（x）=sin（ωx﹣φ）， 的图象经过点 ，且相邻两条对称轴的距离为 ． （Ⅰ）求函数f（x）的解析式及其在[0，π]上的单调递增区间；
（Ⅱ）在△ABC中，a，b，c分别是A，B，C的对边，若 ，求∠A的大小．

Answer 1

【答案】解：（Ⅰ）由相邻两条对称轴的距离为 ，可得其周期为 ，∴ω=2． 则f（x）=sin（2x﹣φ）
∵图象过点 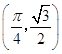，且 ，坐标带入：
得： =sin（2× ﹣φ），即cosφ= ．
∴φ=
那么：函数f（x）的解析式为：f（x）=sin（2x﹣ ）
由 ，k∈Z．
可得：
∴x在[0，π]上增区间为 和 ．
（Ⅱ）由 ，可得 ，
则 ，
得
由于0＜A＜π，
则 ，
那么：
∴ ．
【解析】（Ⅰ）根据相邻两条对称轴的距离为 ，可得周期，从而求出ω，图象过点 ，带入求出φ，即可求函数f（x）的解析式及其在[0，π]上的单调递增区间．（Ⅱ）根据 ，利用三角函数公式化简可得∠A的大小．