题目内容
不等式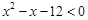 的解集为________.
的解集为________.
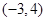
解析试题分析:因为由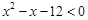 可知其函数
可知其函数 ,则根为-3,4,然后开口向上,则不等式
,则根为-3,4,然后开口向上,则不等式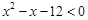 的解集为
的解集为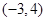 ,故答案为
,故答案为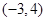 。
。
考点:一元二次不等式的解集
点评:解决该试题的关键是利用给定的不等式,因式分解得到根,然后结合二次函数的 图形得到结论,属于基础题。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
不等式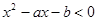 的解集为
的解集为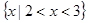 ,则不等式
,则不等式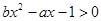 的解集为( )
的解集为( )
| A.(2,3) | B.(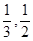 ) ) | C.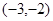 | D.(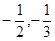 ) ) |
若不等式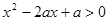 ,对
,对 恒成立,则关于
恒成立,则关于 的不等式
的不等式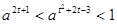 的解集为( )
的解集为( )
A. | B. | C. | D.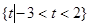 |
设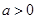 ,不等式
,不等式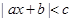 的解集是
的解集是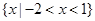 ,则
,则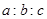 等于( )
等于( )
A.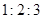 | B.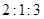 | C.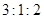 | D.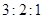 |
如果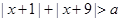 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )
A. | B. | C. | D.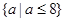 |
不等式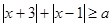 对任意实数
对任意实数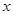 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A.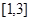 | B. | C.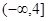 | D.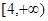 |
不等式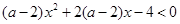 对一切
对一切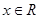 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A.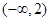 | B.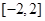 | C.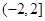 | D.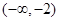 |
当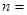 1,2,3,4,5,6时,比较
1,2,3,4,5,6时,比较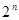 和
和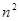 的大小并猜想( )
的大小并猜想( )
A.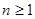 时, 时,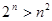 | B.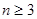 时, 时,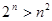 |
C.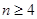 时, 时,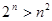 | D.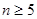 时, 时,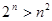 |
不等式 的解集是
的解集是
A. | B. |
C. | D. 或 或 或 或 |