题目内容
设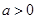 ,不等式
,不等式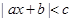 的解集是
的解集是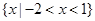 ,则
,则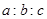 等于( )
等于( )
A.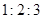 | B.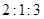 | C.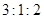 | D.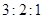 |
B
解析试题分析:先利用绝对值不等式的解法表示出不等式|ax+b|<c的解集,通过不等式解集与对应方程的根的关系,得出方程的根,然后根据韦达定理列出方程中的参数a,b,c的关系式,即可求出a:b:c.根据题意,由于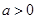 ,不等式
,不等式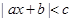 的解集是
的解集是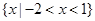 ,则可知
,则可知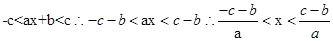 ,那么根据解集对应相等得到
,那么根据解集对应相等得到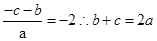 ,
,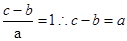 .联立方程组得到
.联立方程组得到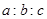 =
=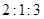 ,故选B.
,故选B.
考点:绝对值不等式
点评:本题考查绝对值不等式,实际上是考查绝对值不等式解集与所对应方程根的关系,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
一元二次不等式 的解集是
的解集是 ,则
,则 的值是( )
的值是( )
A.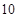 | B.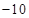 | C.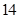 | D.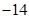 |
不等式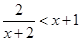 的解集是( )
的解集是( )
A.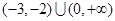 |
B.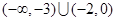 |
C.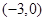 |
D.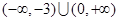 |
设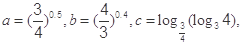 则( ).
则( ).
A.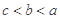 | B.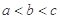 | C.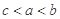 | D.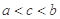 |
已知不等式 的解集为
的解集为 ,
,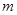 是二项式
是二项式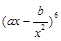 的展开式的常数项,那么
的展开式的常数项,那么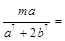
A.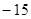 | B.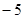 | C.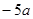 | D. |
设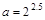 ,
,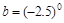 ,
,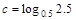 ,则
,则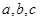 的大小关系是( )
的大小关系是( )
A.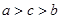 | B.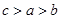 | C.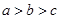 | D.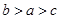 |
不等式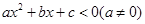 的解集为
的解集为 ,那么( )
,那么( )
A.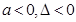 | B.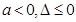 | C.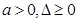 | D.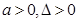 |
不等式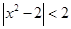 的解集是( )
的解集是( )
A. | B.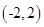 | C. | D.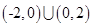 |
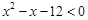 的解集为________.
的解集为________.