题目内容
直线l:y=k(x-2)+2与圆C:x2+y2-2x-2y=0相切,则直线l的斜率为( ).
| A.-1 | B.-2 | C.1 | D.2 |
A
解析

练习册系列答案
相关题目
已知圆的半径为2,圆心在 轴的正半轴上,且与
轴的正半轴上,且与 轴相切,则圆的方程是( )
轴相切,则圆的方程是( )
A. | B. |
C.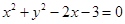 | D. |
直线 将圆
将圆 分割成的两段圆孤长之比为( )
分割成的两段圆孤长之比为( )
A. | B. | C. | D.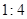 |
若直线 和圆
和圆 相切与点
相切与点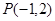 ,则
,则 的值为( )
的值为( )
A.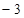 | B. | C. | D. |
圆C1:x2+y2+2x-3=0和圆C2:x2+y2-4y+3=0的位置关系为( )
| A.相离 | B.相交 | C.外切 | D.内含 |
“a=b”是“直线y=x+2与圆(x-a)2+(x-b)2=2相切”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若圆心在x轴上、半径为 的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( ).
的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( ).
A.(x- )2+y2=5 )2+y2=5 |
B.(x+ )2+y2=5 )2+y2=5 |
| C.(x-5)2+y2=5 |
| D.(x+5)2+y2=5 |
 是半径为1的圆的直径,在AB上的任意一点M,过点M作垂直于AB的弦,则弦长大于
是半径为1的圆的直径,在AB上的任意一点M,过点M作垂直于AB的弦,则弦长大于 的概率是 ( )
的概率是 ( )

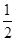

 和
和 是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在
是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在 ,则过A、B、C三点的动圆所形成的图形面积为( )
,则过A、B、C三点的动圆所形成的图形面积为( ) B.
B. C.
C.  D.
D. 