题目内容
【题目】某群体的人均通勤时间,是指单日内该群体成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() 的成员自驾时,自驾群体的人均通勤时间是
的成员自驾时,自驾群体的人均通勤时间是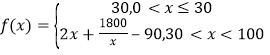 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为40钟,根据上述分析结果回答下列问题:
影响,恒为40钟,根据上述分析结果回答下列问题:
(1)请你说明,当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由题意知求出f(x)>40时x的取值范围即可;
(2)分段求出g(x)的解析式,判断g(x)的单调性,再说明其实际意义
由题意知,
当0<x![]() 30时,f(x)=30<40, 公交群体的人均通勤时间恒大于自驾群体的人均通勤时间;
30时,f(x)=30<40, 公交群体的人均通勤时间恒大于自驾群体的人均通勤时间;
当30<x<100时,![]() >40,
>40,
即x2-65x+900>0,解得x<20(舍去)或x>45
∴ 当x∈(45,100)时,公交群体的人均通勤时间少于自驾群体的人均通勤时间.
(2)当0<x≤30时,g(x)=30x%+40(1-x%)=40-![]()
当30<x<100时,![]() ;
;
∴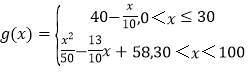
∵当0<x≤30时, g(x)=40-![]() 是单调递减函数,g(30)=37,
是单调递减函数,g(30)=37,
当30<x<100时,![]()
![]() ,且g(30)=37,
,且g(30)=37,
∴当0<x<32.5时,g(x)单调递减;当32.5<x<100时,g(x)单调递增;
实际意义:说明该地上班族S中小于32.5%的人自驾时,随着自驾占比增大,人均通勤时间是递减的;大于32.5%的人自驾时,随着自驾占比增大,人均通勤时间是递增的;当自驾人数为32.5%时,人均通勤时间最短

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目