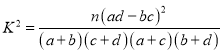题目内容
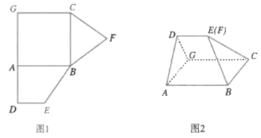
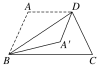
【题目】在等腰梯形ABCD中,已知AB=AD=CD=1,BC=2,将△ABD沿直线BD翻折成△A′BD,如图,则直线BA′与CD所成角的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据翻折过程中∠A′BD=30°,BA′可以看成以B为顶点,BD为轴的圆锥的母线,将问题转化为圆锥的母线与底面内的直线所成角的取值范围.
由题:在等腰梯形ABCD中,已知AB=AD=CD=1,BC=2,
取BC中点M,连接AM,易得四边形AMCD是平行四边形,所以AM=DC=AB,
所以△ABM是等边三角形,则∠ABC=60°,∠ABD=30°,∠A′BD=30°,CD⊥BD,
在翻折过程中,BA′绕着BD旋转,BA′可以看成以B为顶点,BD为轴的圆锥的母线,
CD为圆锥底面内的直线,
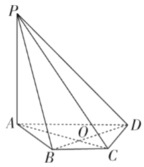
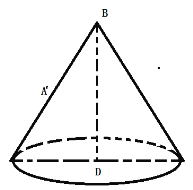
将本问题转化为求解如图圆锥中母线与底面直线所成角的取值范围,
其中母线与轴夹角为30°,所以母线与底面直线所成角的取值范围为![]()
故选:A

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家,京剧艺术大师梅兰芳先生,某电视台《我爱京剧》的一期比赛中,2位“梅派”传人和4位京剧票友(资深业余爱好者)在幕后登台演唱同一曲目《贵妃醉酒》选段,假设6位演员的演唱水平相当,由现场40位大众评委和“梅派”传人的朋友猜测哪两位是真正的“梅派”传人.
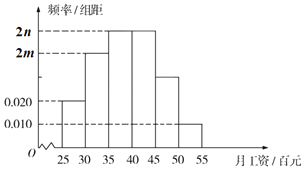
(1)此栏目编导对本期的40位大众评委的年龄和对京剧知识的了解进行调查,根据调查得到的数据如下:
京剧票友 | 一般爱好者 | 合计 | |
50岁以上 | 15 | 10 | 25 |
50岁以下 | 3 | 12 | 15 |
合计 | 18 | 22 | 40 |
试问:在犯错误的概率不超过多少的前提下,可以认为年龄的大小与对京剧知识的了解有关系?
(2)若在一轮中演唱中,每猜出一位亮相一位,且规定猜出2位“梅派”传人”或猜出5人后就终止,记本轮竞猜一共竞猜![]() 次,求随机变量
次,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考数据:
0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
0.05 | 0.025 | 0.005 | 0.001 | |
3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]()