题目内容
选修4-1:几何证明选讲如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB、FC.

(Ⅰ)求证:FB=FC;
(Ⅱ)求证:FB2=FA·FD;

(Ⅰ)求证:FB=FC;
(Ⅱ)求证:FB2=FA·FD;
(Ⅰ)证明略。(Ⅱ)证明略
(Ⅰ)∵AD平分ÐEAC,∴ÐEAD=ÐDAC.
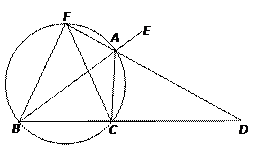
∵四边形AFB C内接于圆,∴ÐDAC=ÐFBC.
C内接于圆,∴ÐDAC=ÐFBC.
∵ÐEAD=ÐFAB=ÐFCB,∴ÐFBC=ÐFCB,
∴FB=FC. -----(5分)
(Ⅱ)∵ÐFAB=ÐFCB=ÐFBC,ÐAFB=ÐBFD,
∴ΔFBA∽ΔFDB.∴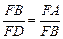 ,∴FB2=FA·FD.-----(10分)
,∴FB2=FA·FD.-----(10分)
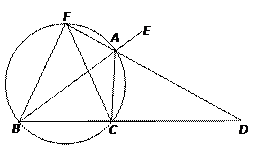
∵四边形AFB
 C内接于圆,∴ÐDAC=ÐFBC.
C内接于圆,∴ÐDAC=ÐFBC.∵ÐEAD=ÐFAB=ÐFCB,∴ÐFBC=ÐFCB,
∴FB=FC. -----(5分)
(Ⅱ)∵ÐFAB=ÐFCB=ÐFBC,ÐAFB=ÐBFD,
∴ΔFBA∽ΔFDB.∴
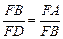 ,∴FB2=FA·FD.-----(10分)
,∴FB2=FA·FD.-----(10分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
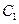 :
: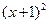 +
+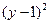 =1,圆
=1,圆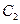 与圆
与圆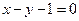 对称,则圆
对称,则圆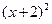 +
+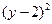 ="1"
="1"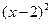 +
+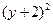 =1
=1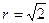 ,BC=1,求AD。
,BC=1,求AD。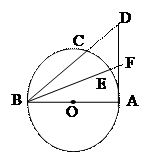
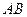 与
与 是
是 的直径,
的直径,
 是
是 交
交 ,连
,连 交
交 ,若
,若 ,则
,则 .
.
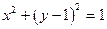 ,
,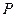 为圆上任意一点(不包括原点)。直线
为圆上任意一点(不包括原点)。直线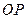 的倾斜角为
的倾斜角为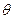 弧度,
弧度,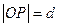 ,则
,则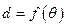 的图象大致为
的图象大致为
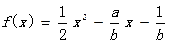 在
在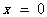 处的切线
处的切线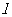 与圆
与圆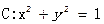 相离,则
相离,则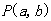 与圆
与圆 的位置关系是( )
的位置关系是( )