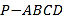题目内容
【题目】四棱锥![]() 与直四棱柱
与直四棱柱![]() 组合而成的几何体中,四边形
组合而成的几何体中,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)动点![]() 在线段
在线段![]() 上(包括端点),若二面角
上(包括端点),若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析(2)![]()
【解析】
(1)在矩形![]() 中,根据
中,根据![]() ,得
,得![]() ,可证
,可证![]() ,又根据
,又根据![]() 为正三角形及面面垂直性质定理可证
为正三角形及面面垂直性质定理可证![]() 平面
平面![]() ,即得
,即得![]() ,由此可证明
,由此可证明![]() 平面
平面![]() ;
;
(2)以![]() 为原点,建立空间直角坐标系,设出点Q坐标,由二面角
为原点,建立空间直角坐标系,设出点Q坐标,由二面角![]() 的余弦值为
的余弦值为![]() ,可解出Q,即可求
,可解出Q,即可求![]() 的长度.
的长度.
(1)矩形![]() 中,
中,![]() ,
,
![]() ,
,
![]() .
.
![]() 四边形
四边形![]() 是菱形,且
是菱形,且![]() ,
,
![]() ,
,
![]() 为正三角形.
为正三角形.
![]() 为
为![]() 的中点,
的中点,
![]() .
.
![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,
![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向建立如图所示的空间直角坐标系,
轴正方向建立如图所示的空间直角坐标系,

则![]() ,
,
设Q![]() ,
,![]() ,
,
则![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则
 ,
,
取![]() ,则
,则![]() .
.
同理求得平面![]() 的一个法向量为
的一个法向量为![]() .
.
![]()
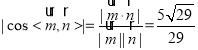
代入
化简即为![]() ,
,
由![]() ,可得
,可得![]() ,
,
故![]() 与
与![]() 重合,
重合,![]() .
.

练习册系列答案
相关题目
【题目】根据我市房地产数据显示,今年我市前5个月新建住宅销售均价逐月上升,为抑制房价过快上涨,政府从6月份开始推出限价房等宏观调控措施,6月份开始房价得到很好的抑制,房价回落.今年前10个月的房价均价如表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
均价y(万元/平方米) | 0.83 | 0.95 | 1.00 | 1.05 | 1.17 | 1.15 | 1.10 | 1.06 | 0.98 | 0.94 |
地产数据研究发现,从1月份至5月份的各月均价y(万元/平方米)与x之间具有正线性相关关系,从6月份至10月份的各月均价y(万元/平方米)与x之间具有负线性相关关系.
(1)若政府不调控,根据前5个月的数据,求y关于x的回归直线方程,并预测12月份的房地产均价.(精确到0.01)
(2)政府调控后,从6月份至10月份的数据可得到y与x的回归直线方程为:![]() .由此预测政府调控后12月份的房地产均价.说明政府调控的必要性.(精确到0.01)
.由此预测政府调控后12月份的房地产均价.说明政府调控的必要性.(精确到0.01)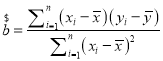 ;
;![]() ;
;